I'm reading this lecture on Linear, Ridge Regression, and PCA. In slide 10 it says that:
The things that I don't understand is the 5th statement which says that $\mathbf{y} - \mathbf{\hat{y}} $ is perpendicular to the subspace. Why is this the case?
I'm reading this lecture on Linear, Ridge Regression, and PCA. In slide 10 it says that:
The things that I don't understand is the 5th statement which says that $\mathbf{y} - \mathbf{\hat{y}} $ is perpendicular to the subspace. Why is this the case?
You have to think about it geometrically in terms of vectors and distances between them!
To understand the idea refer to the next slide:
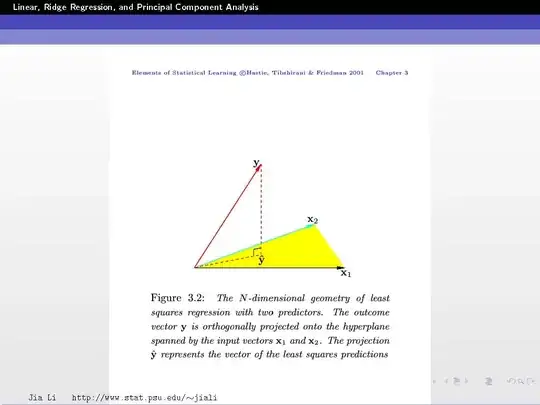
In this example, you have two feature vectors $\mathbf{x}_1$ and $\mathbf{x}_2$ (so $p=2$). These vectors are in 3D space (so $N=3$).
The vector $\mathbf{y}$ is a vector in this 3D space and is given!
The goal is to find the linear combination $\hat{\mathbf{y}}$ (i.e. finding the coefficients $\beta_j$, refer to previous slides) of $\mathbf{x}_1$ and $\mathbf{x}_2$ that allows you to get as close as possible to $\mathbf{y}$.
Back to the example, since you have only 2 feature vectors $\mathbf{x}_1$ and $\mathbf{x}_2$, all their possible linear combinations (from which we will choose one that becomes $\hat{\mathbf{y}}$) will form a plane. We call it the span of the two vectors. This means that $\hat{\mathbf{y}}$ can only live on this plane.
The trick to understand now is to think of $\hat{\mathbf{y}}$ and $\mathbf{y}$ as geometric vectors not only algebraic vectors.
Let's note $\mathbf{e}=\mathbf{y} - \hat{\mathbf{y}}$ which is equivalent to writing $\mathbf{y} = \hat{\mathbf{y}}+\mathbf{e}$ which geometrically means that to get $\mathbf{y}$ you have to add $\mathbf{e}$ to $\hat{\mathbf{y}}$ and $\mathbf{e}$ then represents what separates $\hat{\mathbf{y}}$ from $\mathbf{y}$. Its modulus represents the distance between the two vectors $\hat{\mathbf{y}}$ and $\mathbf{y}$. Patience, we are almost there... :-)
The goal is to minimize this distance. If you refer the the figure above and imagine moving around your $\hat{\mathbf{y}}$ vector inside the subspace spanned by $\mathbf{x}_1$ and $\mathbf{x}_2$ (i.e. the plane) (you also have to imagine $\mathbf{e}$ moving with it going from the head of the vector $\hat{\mathbf{y}}$ to the head of the vector $\mathbf{y}$), then, where do you think that the distance will be minimal?
This happens when $\hat{\mathbf{y}}$ is just under $\mathbf{y}$ such that $\mathbf{e}$ becomes perpendicular to the subspace.
Conclusion:
Minimizing the distance (technically the squared distance) between $\hat{\mathbf{y}}$ and $\mathbf{y}$ is equivalent to having the vector representing this distance perpendicular to the subspace spanned by the feature vectors!
If you prefer an algebraic answer to the +1 geometric answer by MedNait, note that $$ y-\hat y=My $$ with $M=I-X(X'X)^{-1}X'$ the "residual maker matrix". Then, $$MX=X-X(X'X)^{-1}X'X=X-X=0$$