5

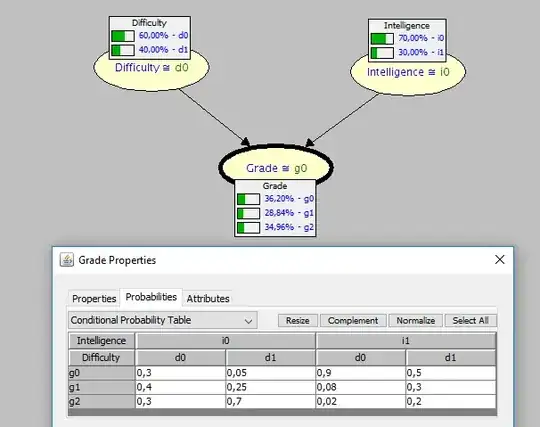
I am now starting to use pgmpy lib for probabailistic graphical model implementation. The probability that I get using this lib differs from the one I get manually (e.g. using SamIam). Here is a screenshot of the very small graphical model made in SamIam to check the concept idea:

Student example

The code I have using pgmpy.

from pgmpy.models import BayesianModel
from pgmpy.factors import TabularCPD
from pgmpy.inference import BeliefPropagation

student_model = BayesianModel([('D', 'G'), ('I', 'G')])

difficulty_cpd = TabularCPD(variable='D', variable_card=2, values=[[0.6, 0.4]])
intel_cpd = TabularCPD(variable='I', variable_card=2, values=[[0.7, 0.3]])
grade_cpd = TabularCPD(variable='G',variable_card=3, values=[[0.3, 0.05, 0.9, 0.5], [0.4, 0.25, 0.08, 0.3], [0.3, 0.7, 0.02, 0.2]], evidence=['I', 'D'], evidence_card=[2, 2])

student_model.add_cpds(grade_cpd, difficulty_cpd, intel_cpd)

print (student_model.nodes())
print (student_model.get_cpds('D'))
print (student_model.get_cpds('I'))
print (student_model.get_cpds('G'))

belief_propagation = BeliefPropagation(student_model)
res = belief_propagation.query(variables=["G"])
print (res['G'])

I get following results

code output

The values of phi(G) are not the same as in Samiam.

According the algorithm used in Samiam we should get for G_0:

P(G_0) = P(G_0|I_0,D_0) + P(G_0|I_0,D_1) + P(G_0|I_1,D_0) + P(G_0|I_1,D_1)
P(G_0) = 0.3*0.7*0.6 + 0.05*0.7*0.4 + 0.9*0.3*0.6 + 0.5*0.3*0.4 = 0.3620

Could someone please give me a tip on how these phi(G) values have been counted (which algorithm is really used), and how I could get the same values as in SamIam.

Olga
  • 53
  • 3

1 Answers1

3

actually, I get the same answer as SamIam when running the nearly the exact same code using the most recent version of pgmpy. The only change I needed to make was that TabularCPD has been refactored so that you now need to declare this import statement:

from pgmpy.factors.discrete import TabularCPD

instead of 

from pgmpy.factors import TabularCPD

['I', 'G', 'D']
╒═════╤═════╕
│ D_0 │ 0.6 │
├─────┼─────┤
│ D_1 │ 0.4 │
╘═════╧═════╛
╒═════╤═════╕
│ I_0 │ 0.7 │
├─────┼─────┤
│ I_1 │ 0.3 │
╘═════╧═════╛
╒═════╤═════╤══════╤══════╤═════╕
│ I   │ I_0 │ I_0  │ I_1  │ I_1 │
├─────┼─────┼──────┼──────┼─────┤
│ D   │ D_0 │ D_1  │ D_0  │ D_1 │
├─────┼─────┼──────┼──────┼─────┤
│ G_0 │ 0.3 │ 0.05 │ 0.9  │ 0.5 │
├─────┼─────┼──────┼──────┼─────┤
│ G_1 │ 0.4 │ 0.25 │ 0.08 │ 0.3 │
├─────┼─────┼──────┼──────┼─────┤
│ G_2 │ 0.3 │ 0.7  │ 0.02 │ 0.2 │
╘═════╧═════╧══════╧══════╧═════╛
╒═════╤══════════╕
│ G   │   phi(G) │
╞═════╪══════════╡
│ G_0 │   0.3620 │
├─────┼──────────┤
│ G_1 │   0.2884 │
├─────┼──────────┤
│ G_2 │   0.3496 │
╘═════╧══════════╛
Djinnome
  • 46
  • 3
  • When I installed pgmpy using pip, I got the same incorrect result as you. It was only when I installed from https://github.com/pgmpy/pgmpy that I got the same answer as samIam. – Djinnome Oct 18 '16 at 18:56
  • Also, I got the same answer as SamIam whether using python2 or python3 as long as I used the github.com/pgmpy/pgmpy version – Djinnome Oct 18 '16 at 18:58
  • 1
    Thank you for your help. I have installed the version of the lib from GitHub and looks like the calculations are right now – Olga Oct 19 '16 at 09:41