Predicting with GLM using Gaussian distributed data

Question

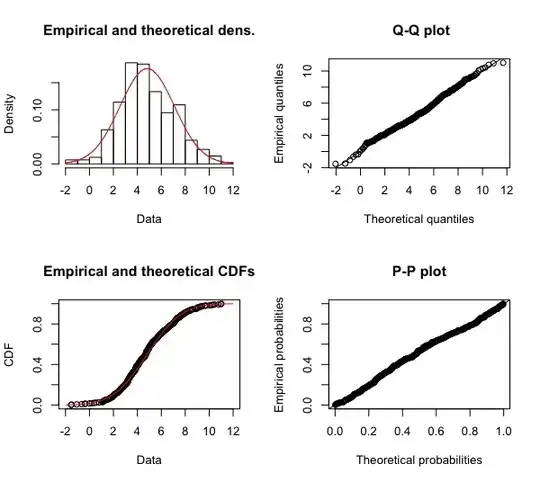
So I have this data from of 26 predictors and 418 observations which I want to use to predict an outcome that is normally distributed (and continuous). The outcome variable looks like this when compared to the theoretical Gaussian distribution:

But for some reason the GLM model I’ve created for it does not predict it very well. I used Gaussian family with identity link and reduced the amount of predictors to only the most significant ones (p < 0.05).

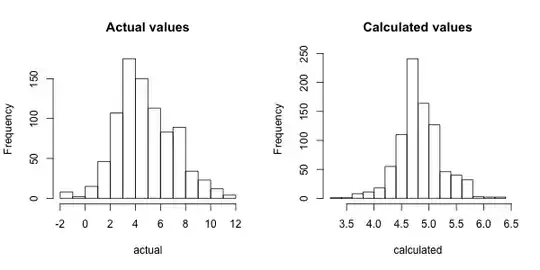
Some cross validation results:

It seems that the distribution of the prediction is too ”thin” – it doesn’t predict anything outside the interval of [3.5, 6.5]. What am I doing wrong? First I thought that Gaussian family was not the correct one for this model but the results on the first picture speak for it. It looks like the model squeezes the prediction distribution because it’s form is very similar to the actual one.

EDIT 2016/10/20: After some research and tons of google searches I came across this question and it's answer: Assumptions of generalised linear model. It helped me a bunch in my understanding of this subject. Apparently the distribution of the dependent variable is not that important to analyse when GLM is in question, but rather the homoscedasticity of variables and the normality of residuals.

Answer 1

Generalized linear model with Gaussian family is a linear regression. I would argue that there is nothing strange about your results. Recall that simple linear regression model is

$$ y_i = \alpha + \beta x_i + \varepsilon_i $$

it could be written differently, in probabilistic notation as

$$ y_i \sim \mathcal{N}(\mu_i, \sigma^2) \\ \mu_i = \alpha + \beta x_i $$

so you can say that $\varepsilon_i$ follows the $\mathcal{N}(0, \sigma^2)$ distribution, where $\sigma^2$ is residual variance.

What follows is that in fact you are not predicting the $y_i$, but rather expected value of $y_i$ conditional on your data and the parameters,

$$ \hat y_i = \hat\mu_i = \hat\alpha + \hat\beta x_i $$

So you should not expect your predictions to resemble the distribution of $y_i$ as you are predicting only the expected values $\mu_i$. Moreover, the variance of predicted values $\hat y_i$ is just a variance of $\mu_i$.

This will get more clear if you look on the plot below: it shows $x_i$ values against $y_i$ values (black points), with corresponding regression line and the predicted values (red line and red points). As you can see, we are fitting the line that best fits "in the middle" of the cloud of datapoints rather then predicting the points themselves.

If you wanted your outcome to resemble $y_i$'s in distribution, then you could conduct a simulation by adding the $\mathcal{N}(0, \sigma^2)$ noise to your predictions, like on the plot below. As you can imagine, such simulated draws would be suboptimal as predictions for individual values (since you add random noise to optimal predictions) while in total being closer in distribution to $y_i$'s.