I need to calculate the prevalence, bias, positive agreement and negative agreement (or other similar meansure) related to Kappa in a matrix with size 3 x 3.
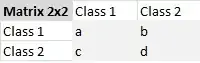
I consulted several papers, but they only calculate it for a 2 x 2 matrix, as below.
Confusion Matrix
positive agreement = (2*a)/(N+a-d)
negative agreement = (2*d)/(N-a+d)
prevalence =[(a+b)/n+(a+c)/n]/2-[(c+d)/n+(b+d)/n]/2 =(a-d)/n
Bias =(a+b)/n-(a+c)/n=(b-c)/n
Thank you!!
Positive Agreement and Negative Agreement are special cases of Specific Agreement:
$$SA(k)=\frac{\sum_{i=1}^{n'}r_{ik}(r_{ik}-1)}{\sum_{i=1}^{n'}r_{ik}(r_i-1)}$$
where $n'$ is the number of items that were coded by two or more raters, $r_{ik}$ is the number of raters that assigned item $i$ to category $k$, and $r_i$ is the number of raters that assigned item $i$ to any category.
To get Positive Agreement, calculate $SA(+)$ and to get negative agreement, calculate $SA(-)$.
One possible solution about an agreement index in this case is to use the Randolph's Kappa (2005).
Another possibility is the kappa-q and kappa-BP (Gwent, 2014), a generalization of Bennet's S, as discussed in this link: free-marginal multirater/multicategories agreement indexes and the K categories PABAK
Consult: "Agree or Disagree? A Demonstration of An Alternative Statistic to Cohen’s Kappa for Measuring the Extent and Reliability of Agreement between Observer" Qingshu Xie (2013)
Positive Agreement and Negative Agreement was addressed by Jeffrey Girard above.
Something similar to Bias and Prevalence may be obtained using the Stuart-Maxwell Test and the McNemar test: http://www.john-uebersax.com/stat/mcnemar.htm#intro
