Proof of variance of stationary time series

Question

Suppose that $\{X_t\}$ is a weakly stationary time series with mean $\mu = 0$ and a covariance function $\gamma(h)$, $h \geq 0$, $\mathrm{E}[X_t] = \mu = 0$ and $\gamma(h)= \operatorname{Cov}\left(X_t, X_{t + h}\right) = \mathrm{E}\left[X_tX_{t + h}\right]$

Show that:

$$ \operatorname{Var}\left( \frac{X_1 + X_2 +\ldots+ X_n}{n}\right) = \frac{\gamma(0)}{n} + \frac{2}{n}\sum_{m=1}^{n-1} \left( 1−\frac{m}{n}\right)\gamma(m). $$

So far, I've gotten this:

\begin{align} \operatorname{Var}(\bar X ) &= \frac{1}{n^2} \sum_{i=1}^{n} \sum_{j=1}^{n} \operatorname{Cov}(X_i,X_j) \\[7pt] &= \frac{1}{n^2} \sum_{i-j=-n}^{n} (n-|i-j|)\gamma(i-j) \\[7pt] &= \frac{1}{n} \sum_{m=-n}^{n} \left(1- \frac{|m|}{n}\right)\gamma (m) \end{align} How am I supposed to come up with the $\frac{\gamma(0)}{n} + \frac{2}{n}$?

Answer 1

You are almost there! Now you just need to recognise that auto-correlation only depends on the lag, so you have $\gamma(m) = \gamma(|m|)$, which means that the entire summand depends on $m$ only through $|m|$ (i.e., it is symmetric around $m=0$). This allows you to split the sum into the middle element ($m=0$) and two lots of the symmetric part ($|m| = 1,...,n$), which gives you:

$$\begin{equation} \begin{aligned} \text{Var}(\bar{X}) &= \frac{1}{n} \sum_{m=-n}^{n} \Big( 1-\frac{|m|}{n} \Big) \gamma(m) \\[6pt] &= \frac{1}{n} \sum_{m=-n}^{n} \Big( 1-\frac{|m|}{n} \Big) \gamma(|m|) \\[6pt] &= \frac{1}{n} \Bigg[ \gamma(0) +2\sum_{|m|=1}^n \Big( 1-\frac{|m|}{n} \Big) \gamma(|m|) \Bigg] \\[6pt] &= \frac{\gamma(0)}{n} + \frac{2}{n} \sum_{m=1}^n \Big( 1-\frac{m}{n} \Big) \gamma(m) \\[6pt] &= \frac{\gamma(0)}{n} + \frac{2}{n} \sum_{m=1}^{n-1} \Big( 1-\frac{m}{n} \Big) \gamma(m). \\[6pt] \end{aligned} \end{equation}$$

(The last step follows from the fact that $1-\tfrac{m}{n} = 0$ for $m=n$.) This method of splitting symmetric sums around their mid-point is a common trick used in these kinds of cases to simplify the sum by taking it only over positive arguments. It is a worthwhile trick to learn in general.

Answer 2

Since this post has attracted so many answers, it seems worthwhile to show the idea.

Here is a diagram of the covariance matrix $\Sigma = \operatorname{Cov}(X_1,X_2,\ldots, X_n).$ Values that are necessarily equal receive the same color. It has this diagonal striped pattern because the covariances depend only on the absolute lags--and the lags index the diagonals.

The variance of a sum of random variables $X_1+\cdots +X_n$ is the sum of all their variances and covariances, taken in all orders. This is a consequence of the multilinear property of covariance. It is easily demonstrated by observing $X_1+\cdots +X_n$ is the dot product of the random vector $\mathbf{X}=(X_1,\cdots,X_n)$ and the vector $\mathbf{1}=(1,1,\ldots 1)$ (with $n$ components). Therefore the variance of the sum is

$$\operatorname{Var}(X_1+\cdots+X_n) = \mathbf{1}^\prime \Sigma \mathbf{1},$$

which the rules of matrix multiplication tell us is the sum of all the entries of $\Sigma.$

The formula in the question sums the entries of $\Sigma$ by color:

1. There are $n$ copies of $\gamma_0$ (in red, on the diagonal).

2. There are $2(n-1)$ copies of $\gamma_1$ (in orange, on both sides of the diagonal: this is where the factor of $2$ comes from).

3. There are $2(n-2)$ copies of $\gamma_2$ (in yellow).

... and so on, up to $2$ copies of $\gamma_{n-1}$ (in blue).

Therefore, by merely looking at the figure, we obtain

$$\operatorname{Var}(X_1+\cdots+X_n) = n\gamma_0 + 2(n-1)\gamma_1 + 2(n-2)\gamma_2 + \cdots + 2\gamma_{n-1}.$$

The general pattern is

There are $n$ copies of $\gamma_0$ and $2(n-m)$ copies of $\gamma_m$ for $m=1,2,\ldots, n-1.$

The question asks for the variance of $1/n$ times this sum. Again, according to the multilinear property of variance, we must multiply the variance of the sum by $1/n^2.$ Doing that to the preceding formula gives the answer,

$$\operatorname{Var}((X_1+\cdots+X_n)/n) = \frac{1}{n^2}\left[n\gamma_0 + \sum_{m=1}^{n-1} 2(n-m)\gamma_m\right].$$

Comparing this to the formula in the question helps us interpret the question's "$1/n$" factors as really being $1/n=n/n^2,$ $(1-1/n)/n= (n-1)/n^2,$ and so on down to $(1-(n-1)/n)/n = 1/n^2.$

Answer 3

first, fixing the definition of the problem, the index is $m$ instead of $u$, to make simpler I will use only the index $i$ and $j$.

We want to prove that

$\operatorname{Var}\left(\frac{X_1+X_2+...+X_n}{n}\right) = \dfrac{\gamma(0)}{n} + \dfrac{2}{n} \sum_{i=1}^{n-1} \left(1−\dfrac{i}{n}\right) \gamma(i).$

The begin is correct,

$$\operatorname{Var}(\bar{X}) = \dfrac{1}{n^2} \sum_{i=1}^n\sum_{j=1}^n \operatorname{Cov}(X_i,X_j)$$

We can notice that $\operatorname{Cov}(X_i,X_j) = \operatorname{Cov}(X_j,X_i)$ and, from our assumptions about the problem, that $\operatorname{Cov}(X_i,X_i+h) = \operatorname{Cov}(X_i,X_i-h) = \gamma(h)$ for any $i$ and $h$.

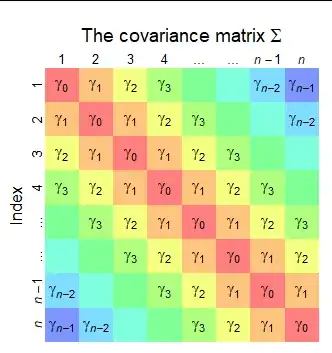
We can visualize the sum of covariances in $i$ and $j$ as follows

$$\left| \begin{array}{ccccc} \operatorname{Cov}(1,1) & \operatorname{Cov}(1,2) & \cdots & \operatorname{Cov}(1,n-1) & \operatorname{Cov}(1,n)\\ \operatorname{Cov}(2,1) & \operatorname{Cov}(2,2) & \cdots & \operatorname{Cov}(2,n-1) & Cov(2,n)\\ \vdots & \vdots & \ddots & \vdots & \vdots\\ \operatorname{Cov}(n-1,1)& \operatorname{Cov}(1,2) & \cdots & \operatorname{Cov}(n-1,n-1) &\operatorname{Cov}(n-1,n)\\ \operatorname{Cov}(n,1) & \operatorname{Cov}(n,2) & \cdots & \operatorname{Cov}(n,n-1) &\operatorname{Cov}(n,n) \end{array} \right|$$

What is equal to

$$\left| \begin{array}{ccccc} \gamma(0) & \gamma(1) & \cdots & \gamma(n-1)\\ \gamma(1) & \gamma(0) & \cdots & \gamma(n-2)\\ \vdots & \vdots & \ddots & \vdots\\ \gamma(n-1)& \gamma(n-2) & \cdots & \gamma(0)\\ \end{array} \right|$$

To sum all the elements we can first sum the main diagonal, and as it is symmetric sum twice the other diagonals

$$\sum_{i=1}^n\sum_{j=1}^n \operatorname{Cov}(X_i,X_j) = n \gamma(0) + 2\sum_{i=1}^{n-1}(n-i)\gamma(i)$$.

Back to the main equation

$$\operatorname{Var}\left(\frac{X_1+X_2+...+X_n}{n}\right) = \dfrac{\gamma(0)}{n}+\dfrac{2}{n^2}\sum_{i=1}^{n-1}(n-i)\gamma(i) = \dfrac{\gamma(0)}{n}+\dfrac{2}{n}\sum_{i=1}^{n-1}(1-\dfrac{i}{n})\gamma(i).$$

Answer 4

We have,

$Var(\bar{X})=Var\left(\frac{\sum\limits_{i=1}^{n}{X_i}}{n}\right)=\frac{1}{n^2}Var\left(\sum\limits_{i=1}^{n}{X_i}\right)=\frac{1}{n^2}\left(\sum\limits_{i=1}^{n}{Var(X_i)}+2\underset{1\leq i<j\leq n}{\sum\sum}cov(X_i,X_j)\right)$

Also, by definition of the covariance function (corresponding to different lag values) of a weakly stationary time series,

we have $\gamma(0)=cov(X_1,X_1)=cov(X_2,X_2)=\ldots=cov(X_n,X_n)$, i.e.,

$\begin{split} \gamma(0)&=&Var(X_1)&=&Var(X_2)&=&\ldots&=&Var(X_n)& \quad \text{there are $n$ terms} \\[-1pt] \gamma(1)&=&cov(X_1,X_2)&=&cov(X_2,X_3)&=&\ldots&=&cov(X_{n-1},X_n) & \quad\text{there are $(n-1)$ terms} \\ \gamma(2)&=&cov(X_1,X_3)&=&cov(X_2,X_4)&=&\ldots&=&cov(X_{n-2},X_n) & \quad\text{there are $(n-2)$ terms} \\ \ldots&&&&\ldots&&&&\ldots& \\ \gamma(n-2)&=&cov(X_1,X_{n-2})&=&cov(X_2,X_{n-1})&&&& & \quad\text{there are $2$ terms} \\ \gamma(n-1)&=&cov(X_1,X_{n-1})&&&&&& & \quad\text{there is $1$ term} \\ \end{split}$

Hence, we have,

$\sum\limits_{i=1}^{n}{Var(X_i)}=n\gamma(0)$ and $\underset{i<j}{\sum\sum}cov(X_i,X_j)=(n-1)\gamma(1)+(n-2)\gamma(2)+\ldots+2\gamma(n-2)+\gamma(n-1)$ $\quad\quad\quad\quad\quad\quad\quad\quad=\sum\limits_{m=1}^{n-1}{(n-m)\gamma(m)}$

$\implies Var(\bar{X})=\frac{1}{n^2}\left(\sum\limits_{i=1}^{n}{Var(X_i)}+2\underset{1\leq i<j \leq n}{\sum\sum}cov(X_i,X_j)\right)$ $\quad\quad\quad\quad\quad\quad=\frac{1}{n^2}\left(n\gamma(0)+2\sum\limits_{m=1}^{n-1}{(n-m)\gamma(m)}\right)$

$\implies Var(\bar{X})=\frac{\gamma(0)}{n}+\frac{2}{n}\sum\limits_{m=1}^{n-1}{(1-\frac{m}{n})\gamma(m)}$