I am working on a data visualization like this NY Times interactive (http://www.nytimes.com/interactive/2014/upshot/buy-rent-calculator.html):
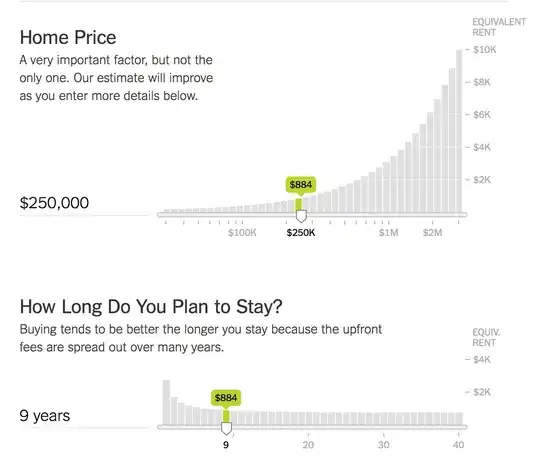 If you go to that link, there are 20 of these charts. I don't know what Mike Bostock and the other authors call this type of charts, but I call them sensitivity charts - how sensitive is a value to a change in a parameter. The green bar is the value and the gray bar is the value if you moved the slider over to it. Some parameter changes don't affect much (gray bars have a small slope), some affect it greatly (large slope).
If you go to that link, there are 20 of these charts. I don't know what Mike Bostock and the other authors call this type of charts, but I call them sensitivity charts - how sensitive is a value to a change in a parameter. The green bar is the value and the gray bar is the value if you moved the slider over to it. Some parameter changes don't affect much (gray bars have a small slope), some affect it greatly (large slope).
The calculations for the linked visualization are simple enough that each gray bar for every chart can be calculated on changes of the slider (~1000 calculations). I've built similar charts before and that technique works great.
Now I'm trying to do it with calculations that take too long to run interactively. Each bar would take ~1min to calculate. So I've looked at a couple approaches:
- Pre-calculate each permutation: This is possible but depending on the step size, I'm looking at ~10M-1B permutations with file sizes over 50GB. That doesn't work on the browser
- Calculate in real-time on GPU: It's pretty difficult for me to port these calculations over to the GPU
What I'm thinking is training some type of regression model that would allow me to generate a pre-trained model. Then the calculation in the browser can be reduced to matrix multiplication. If matrix multiplication isn't fast enough on the CPU, it's relatively easy to port over to the GPU so it can still be interacted with in real-time.
So in other words, I have
- Non-linear functions that can generate as much training data as needed
- 8-10 inputs that I know lower and upper bounds
- Perfect error checking (because I can generate the result I'm checking against)
Would a simple feed-forward neural net deal with this well? I don't have a lot of experiences with the different types of neural nets but would like to get started in the right direction. Or would another type of non-linear regression better deal with this?