2

I have an incomplete dataset where I´m doing a propensity score matched analysis. I´ll be using the approach detailed in Mitre et al and shortly summarized in this post. I´ve thus created 10 imputed dataset, created a propensity-score and in order to demonstrate the effect of matching on the covariate distribution before and after I´ve made a graph.

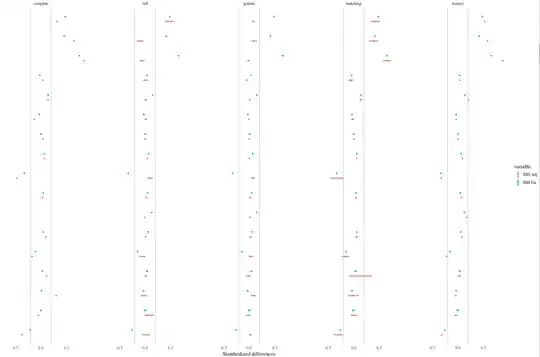
Now - I´m somewhat surprised as to why the range of standardized differences is larger, although better matched, than the unadjusted differences (based on the imputed models). enter image description here

Any idea if this is reasonable?

Community
  • 1
Misha
  • 1,173
  • 1
  • 11
  • 25

1 Answers1

1

My intuition is that since you're using a single propensity score to balance across all imputed data sets, the propensity score isn't responding to the unique characteristics of each data set. That is, if you had used the "within" approach, you wouldn't expect to see such variability because each propensity score within each imputation is responding to the characteristics of its data set. The "across" propensity score might yield totally different matches of varying quality across imputations.

The unadjusted differences don't have this problem to the same degree because no matches are being formed, so the only variability in the differences is coming from the variability in the imputed values.

If you haven't, check out King & Nielson's (2016) paper on why you shouldn't use PS matching (excluding genetic and full). It may explain the poor performance of the PS in your rightmost columns.

Also, based on the names, it looks like you're using cobalt, and if so, thank you very much! I have an update coming out for it soon that will make generating love plots with multiply imputed data quite easy and straightforward. I love the idea of using the bars to represent the variability across imputations.

Noah
  • 20,638
  • 2
  • 20
  • 58
  • Thanks for your reponse and Cobalt. It makes life so much easier comparing across different matching-methods. Looking forward to the nest update. I calculated the imputed datasets using MICE and subsequently did propensity scoring for each of the imputed datasets. My thought is next to average across the propensity scores before doing the final causal effect calculation. By the way, Twang is actually returning the best matches (even better than genetic). Have you ever tried to use the different imputation sets as cluster-IDs to svydesign in survey without averaging? It would have been sweet... – Misha Oct 12 '16 at 21:30
  • I'm actually doing a very similar project. I prefer weighting in general. I generated 25 imputed data sets, and used CBPS within each data set to generate weights. I prefer the "within" approach, so I don't do any averaging of propensity scores; rather, I analyze each data set separately and then combine results using Rubin's rules. For that step, I used Stata, which is very good with multiply imputed data. I prefer the "within" approach because I like to ensure I have balance within each data set; Mitra's paper showed that the advantages to the "across" approach go away when using weighting. – Noah Oct 12 '16 at 22:06
  • Also, thank you for the kind words about cobalt. I don't know if you've updated to the newest version, but if so, you can assess balance on multiply imputed data sets by specifying the imputation number into the cluster option in bal.tab(). The next update focuses specifically on making this operation more powerful. – Noah Oct 12 '16 at 22:08
  • Could you provide an example as to how the cluster option in bal.tab works? I dont quite understand the data structure. I have the different imputation sets as lists within lists as it lends itself perfect to the purrr package. I cannot quite grasp how I would enter the cluster ID´s from this data structure. – Misha Oct 13 '16 at 10:03
  • I used the mice package in R. When you use `complete(imp.data, "long")`, it yields a data set that has a row for each individual and each imputation (so for 10 imputations, you'd have 10 rows for each individual), and each row would have a corresponding imputation number (i.e., whether is was generated from imputation 1, etc.). That imputation can be used with `bal.tab(obj, cluster = data$.imp)` which treats the imputations as clusters. That way you can assess balance across imputations quickly. – Noah Oct 13 '16 at 19:46
  • You can use `purrr`'s `flatten()` to do this easily. – Noah Oct 13 '16 at 19:49
  • I didnt know of the "long" argument to complete. `data("lalonde") lalonde$age[sample(1:614,50)] – Misha Oct 13 '16 at 20:41
  • I opened up a chatroom for us to talk about this further and so I could paste my code. The link is [here](http://chat.stackexchange.com/rooms/46775/propensity-scores-with-missing-data). – Noah Oct 14 '16 at 04:07