Mean = mode doesn't imply symmetry.
Even if mean = median = mode you still don't necessarily have symmetry.
And in anticipation of the potential followup -- even if mean=median=mode and the third central moment is zero (so moment-skewness is 0), you still don't necessarily have symmetry.
... but there was a followup to that one. NickT asked in comments if having all odd moments zero was enough to require symmetry. The answer to that is also no. [See the discussion at the end.$^\dagger$]
Those various things are all implied by symmetry (assuming the relevant moments are finite) but the implication doesn't go the other way - in spite of many an elementary text clearly saying otherwise about one or more of them.
Counterexamples are pretty trivial to construct.
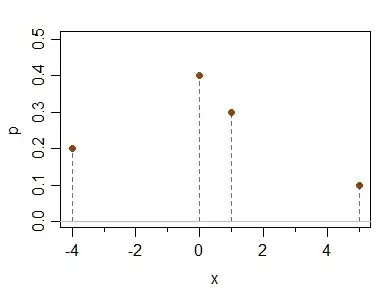
Consider the following discrete distribution:
x -4 0 1 5
P(X=x) 0.2 0.4 0.3 0.1
It has mean, median, mode and third central moment (and hence moment-skewness) all 0 but it is asymmetric.
This sort of example can be done with a purely continuous distribution as well. For example, here's a density with the same properties:
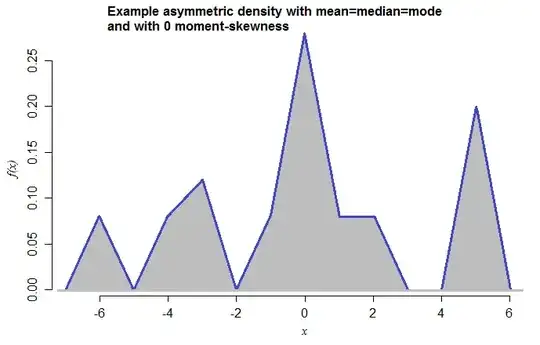
This is a mixture of symmetric triangular densities (each with range 2) with means at
-6, -4, -3, -1, 0, 1, 2, 5 and mixture weights 0.08, 0.08, 0.12, 0.08, 0.28, 0.08, 0.08, 0.20 respectively. The fact that I just made this now -- having never seen it before -- suggests how simple these cases are to construct.
[I chose triangular mixture components in order that the mode would be visually unambiguous -- a smoother distribution could have been used.]
Here's an additional discrete example to address Hong Ooi's questions about how far from symmetry these conditions allow you to get. This is by no means a limiting case, it's just illustrating that it's simple to make a less symmetric looking example:
x -2 0 1 6
P(X=x) 0.175 0.5 0.32 0.005
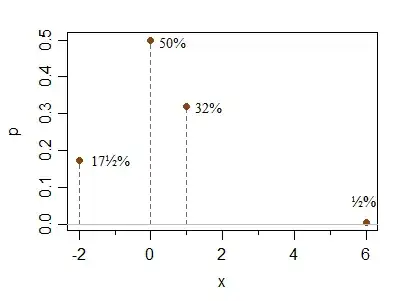
The spike at 0 can be made relatively higher or lower without changing the conditions; similarly the point out to the right can be placed further away (with a reduction in probability) without changing the relative heights at 1 and -2 by much (i.e. their relative probability will stay close to the 2:1 ratio as you move the rightmost element about).
More detail on the response to NickT's question
$\dagger$ The all-odd-moments zero case is addressed in a number of questions on site. There's an example here (see the plot) based on the details here (see toward the end of the answer). That is a continuous unimodal asymmetric density with all odd moments 0 and mean=median=mode. The median is 0 by the 50-50 mixture construction, the mode is 0 by inspection -- all members of the family on the real half-line from which the example is constructed have a density that's monotonic decreasing from a finite value at the origin, and the mean is zero because all odd moments are 0.