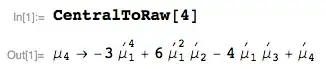It is possible to express central moments in terms of raw moments.
E.g. for skewness we get: $$ {\begin{aligned}\gamma _{1}&=\operatorname {E} \left[\left({\frac {X-\mu }{\sigma }}\right)^{3}\right]\\&={\frac {\operatorname {E} [X^{3}]-3\mu \operatorname {E} [X^{2}]+3\mu ^{2}\operatorname {E} [X]-\mu ^{3}}{\sigma ^{3}}}\\&={\frac {\operatorname {E} [X^{3}]-3\mu (\operatorname {E} [X^{2}]-\mu \operatorname {E} [X])-\mu ^{3}}{\sigma ^{3}}}\\&={\frac {\operatorname {E} [X^{3}]-3\mu \sigma ^{2}-\mu ^{3}}{\sigma ^{3}}}.\end{aligned}} $$
I was wondering how to express kurtosis in terms of raw moments? I came this far:
$$\beta_4= {E} \left[\left({\frac {X-\mu }{\sigma }}\right)^{4}\right]= \frac{E(X^4)-4E(X^3)\mu+6E(X^2)\mu^2-3\mu^4}{(\sigma^2)^2}$$
Hereby I used Binomial expansion to write out the brackets. If this is correct, can the nominator perhaps be more simplified (like in the skewness example where the variance was taken out in step 3)?