Note: I have no readily available source for all of the following, but I have simulations demonstrating everything.
It is a general rule that fitting a regression overall always overfits the training by some amount, and that various goodness-of-fit tests/statistics don't behave the same way in the training sample as in the validation sample. Also, the null hypothesis $H_0$ when applying a goodness-of-fit test is different between the two: in the goodness-of-fit test on the training sample, $H_0$ is generally something like "the regression model (e.g. y~x, y~x+I(x^2), etc.) is appropriate." It doesn't require that the regression parameters themselves are exact. On the other hand, the null hypothesis when applying the test to a validation sample is generally that the parameters are exactly correct, since they haven't been tuned to the sample at hand.
A familiar case in point is linear regression. The mean-square-error (MSE) is always lower in the training sample than a validation sample, for the obvious reason that it has been explicitly minimized in the training sample. Consider the following simulation:
n <- 10
a <- 0.1
b <- 0.5
sigma <- 0.1
nums <- 10000
mse <- data.frame(fit=numeric(nums),raw=numeric(nums))
fitmses <- c()
for (i in 1:nums) {
x <- rnorm(n)
pred <- a+b*x
y <- rnorm(n,pred,sigma)
mse$raw[i] <- mean((y-pred)^2)
fit <- lm(y~x)
pred <- predict(fit)
mse$fit[i] <- mean((y-pred)^2)
}
library(reshape2)
library(ggplot2)
mmse <- melt(mse)
ggplot(mmse,aes(x=value))+
facet_wrap(~variable,scales = "free_x")+
geom_histogram()+
theme_bw()
In this simulation, the true relationship between y and x is $y = 0.1 + 0.5x + \epsilon$ where $\epsilon \sim N(0,0.1)$. Ten thousand simulations with randomly generated x and y are done comparing two quantities: the MSE of fits performed to the sample and the MSE using the correct formula. The two quantities appear somewhat similar:
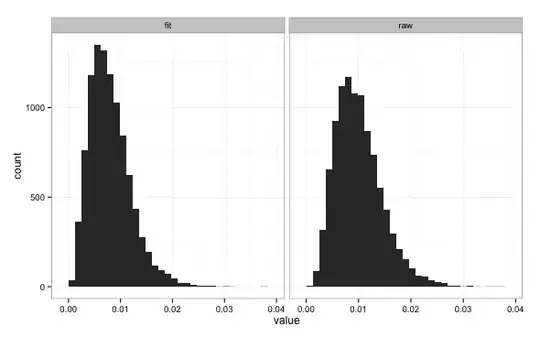
However, the MSE computed with the true coefficient values is always higher than the the fit value (as it should be). You can easily work out that on the validation sample the MSE uses the exact values, times 10 (the number $n$ of entries in the sample) and divided by $\sigma^2$, follows a chi-square distribution with $n=10$ degrees of freedom:
$$
\sum_i \frac{(\hat y_i - y_i)^2}{\sigma^2} = \sum_i\left(\frac{\epsilon}{\sigma} \right)^2
$$
where $\epsilon/\sigma$ is standard normal, and each term is independent (since a fit hasn't been performed to this dataset). Directly showing this,
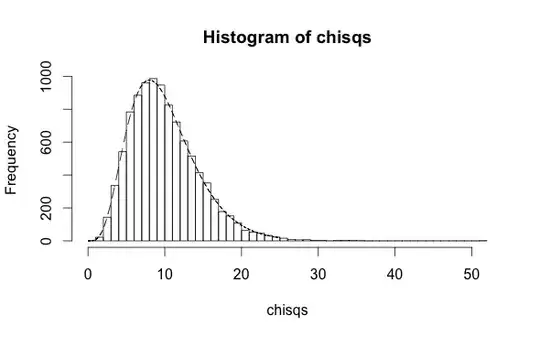
h <- hist(mse$raw*n/sigma^2,50)
x <- seq(0,30,0.1)
y <- dchisq(x,df=n)
scale <- (h$count/h$density)[1]
lines(x,y*scale)
Maybe you can do me one better and show this using fitdistr. Remember that this distribution is demonstrating the null hypothesis: that when the regression parameters are exactly correct, this quantity will follow a chi-square distribution with $n$ degrees of freedom. In practice, if a and b have been determined from a fit to a separate training sample, they won't be exactly correct. Then the null hypothesis is invalid. The effective number of degrees of freedom will actually be higher than $n$, leading to larger values of the MSE and low $p$-values from the chi-square test that could reject the null hypothesis.
The MSE from the fitted values is lower, since it has been explicitly minimized, and the rescaled value follows a chi-square distribution with $n-2$ degrees of freedom:
h <- hist(mse$fit*n/sigma^2,50)
x <- seq(0,30,0.1)
y <- dchisq(x,df=n-2)
scale <- (h$count/h$density)[1]
lines(x,y*scale)

Again, if you doubt this you can check it with fitdistr. [Note: I used the known value of sigma in the above in calculating the above distribution. In reality this quantity would be unknown. The lm fit result contains the estimated sigma, which could be used in place, but I won't be redoing the simulation with this]. The values of a and b don't need to be exact, here, because the null hypothesis is that the model $y=a+bx+\epsilon$ is a good representation of the data, not that a and b are exactly correct. The reduction by $2$ in the degrees of freedom related to the two fit parameters. You can try quadratic, cubic, etc. models with $p$ parameters; the reduction in the d.o.f. will increase with $p$, though it won't be exactly $p$ unless $n \gg p$.
In summary: the very act of performing a regression on a training dataset tries to minimize some quantity measuring the discrepancy between predictions and actual values. This means that measures of discrepancy like goodness-of-fit tests have values that are smaller in training sets than in validation sets.
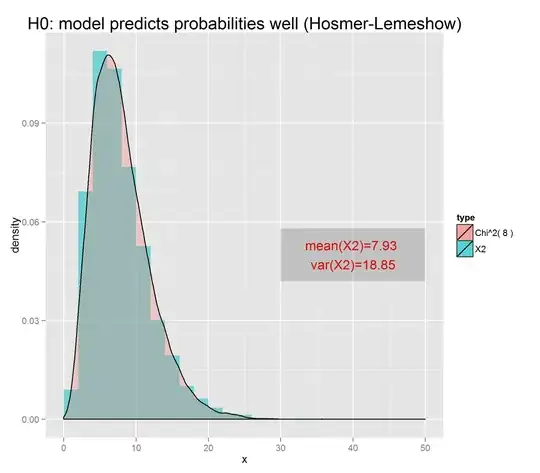
The case of the Hosmer-Lemeshow test for logistic regression is very similar. Here are two small simulations analogous to the above linear regression simulation. In the first, there is an independent variables $x$ and a dependent binary variable $y$. Previous research has shown that the probability that $y$ is true is $\pi = 1/(1+\exp(-[0.1+0.5x]))$. Assuming this is exactly true (the null hypothesis), the following code simulates 10 thousand cross-checks where this prediction is applied to new data and checked against the known values $y$, at each step calculating the Hosmer-Lemeshow statistic. The result follows a chi-square distribution with 10 degrees of freedom -- one for each partition used in the test:
library(ResourceSelection)
n <- 500; chisqs <- c()
for (i in 1:10000) {
x <- rnorm(n)
p <- plogis(0.1+0.5*x)
y <- rbinom(n,1,p)
x2 <- hoslem.test(y,p)$statistic
chisqs <- cbind(chisqs,x2);
}
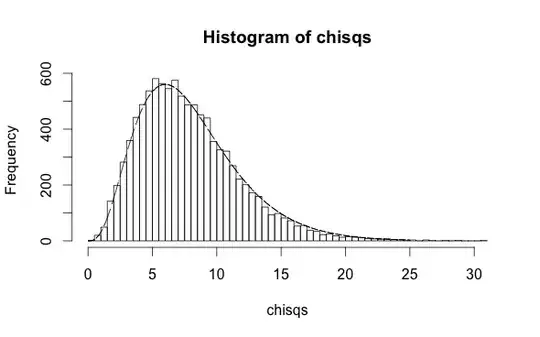
h <- hist(chisqs,50)
xs <- seq(0,25,0.01)
ys <- dchisq(xs,df=10)
lines(xs,ys*h$counts/h$density)
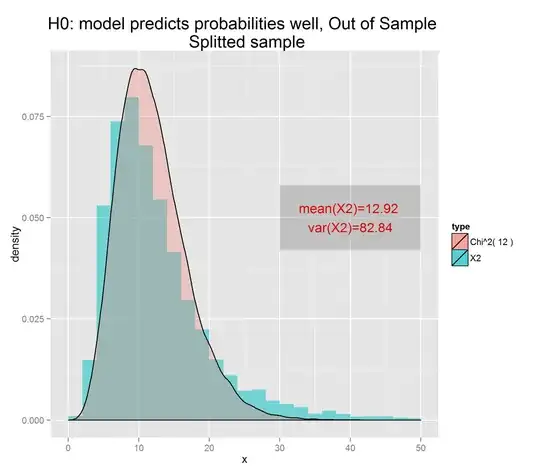
On the other hand, if you use the values of $y$ to make a fit and create the predictions, you'll clearly do better because you've peeked at the answers during the minimization. In this case the degrees of freedom in the distribution of the HL statistic are 8:
library(ResourceSelection)
n <- 500; chisqs <- c()
for (i in 1:10000) {
x <- rnorm(n)
p <- plogis(0.1+0.5*x)
y <- rbinom(n,1,p)
fit <- glm(y~x,family="binomial")
x2 <- hoslem.test(y,fitted(fit))$statistic
chisqs <- cbind(chisqs,x2);
}
h <- hist(chisqs,50)
xs <- seq(0,25,0.01)
ys <- dchisq(xs,df=8)
lines(xs,ys*h$counts/h$density)
This is exactly equivalent to the difference in degrees of freedom for the MSE distributions. Since linear regression is more popular, you're more likely to find sources in the literature verifying what I've claimed and shown here in the linear regression use-case.
In general, you should determine the number of degrees of freedom in the null hypothesis by using simulations like the above. When the number of fit parameters is greater than 2, or when $n$ is not much much greater than $p$, things can start breaking down, and $n-p$ is unlikely to be a good estimate of the degrees of freedom in the training sample. $n$ should always be the number of d.o.f. in the validation sample, however (in the null hypothesis that the regression taken from a different training sample is exactly correct).
EDIT
The number of degrees of freedom is still $g-2$ when doing a logistic regression with a quadratic model with three parameters, contradicting an incorrect claim I made in the comments (and hinted at in this answer where I associated the 2 in $g-2$ with the two fit parameters). In simulation,
library(ResourceSelection)
n <- 500
chisqs <- c()
a <- 0.1
b <- 0.5
c <- 0.2
for (i in 1:10000) {
x2 <- rnorm(n)
p2 <- plogis(a+b*x2+c*x2^2)
y2 <- rbinom(n,1,p2)
fit <- glm(y2~x2+I(x2^2),family="binomial")
stat <- hoslem.test(y2,fitted(fit))$statistic
chisqs <- cbind(chisqs,stat)
}
h <- hist(chisqs,50)
xs <- seq(0,25,0.01)
ys <- dchisq(xs,df=8)
lines(xs,ys*h$counts/h$density)
So, I apologize for this mistake. It does not take away from the rest of the answer, however.
SECOND EDIT
Here is the same quadratic model, on a validation sample, as requested:
library(ResourceSelection)
n <- 500
chisqs <- c()
a <- 0.1
b <- 0.5
c <- 0.2
for (i in 1:10000) {
x2 <- rnorm(n)
p2 <- plogis(a+b*x2+c*x2^2)
y2 <- rbinom(n,1,p2)
stat <- hoslem.test(y2,p2)$statistic
chisqs <- cbind(chisqs,stat)
}
h <- hist(chisqs,50)
xs <- seq(0,25,0.01)
ys <- dchisq(xs,df=10)
lines(xs,ys*h$counts/h$density)
FINAL EDIT
As requested, here is one more simulation, in which the parameters a and b are estimated beforehand from a larger training sample with ten times as many entries. Then applying this fit to the validation samples, the do.f. is still close to 10:
library(ResourceSelection)
n <- 500
chisqs <- c()
a <- 0.1
b <- 0.5
c <- 0.2
x <- rnorm(10*n)
p <- plogis(a+b*x+c*x^2)
y <- rbinom(10*n,1,p)
fit <- glm(y~x+I(x^2),family="binomial")
for (i in 1:10000) {
x2 <- rnorm(n)
p2 <- plogis(a+b*x2+c*x2^2)
y2 <- rbinom(n,1,p2)
stat <- hoslem.test(y2,predict(fit,data.frame(x=x2),type="response"))$statistic
chisqs <- cbind(chisqs,stat)
}
h <- hist(chisqs,50)
xs <- seq(0,25,0.01)
ys <- dchisq(xs,df=10)
lines(xs,ys*h$counts/h$density)
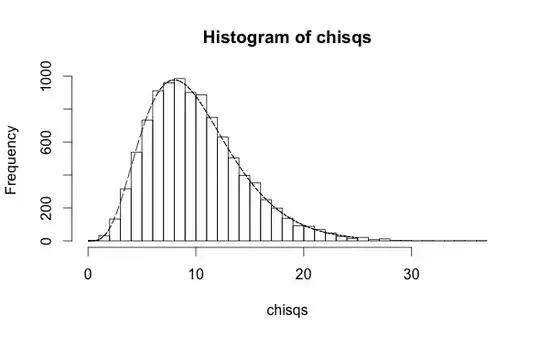
If the number of data points in the training sample (above, 5000) was decreased, the measured parameters a, b, and c would differ from their exact values by more and the null hypothesis would be violated. The distribution of the HL test statistic would no longer be chi-square and would skew higher (making it look like it had $>g$ d.o.f. if you superimposed a chi-square distribution).