3

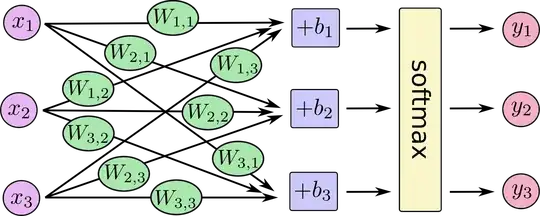
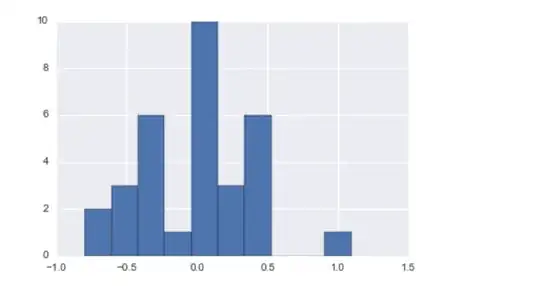
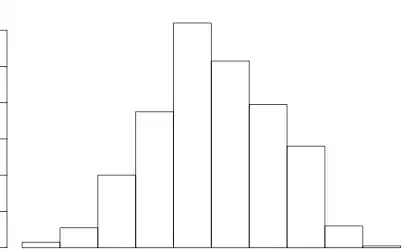
I have a sample dataset where I applied multilinear regression with 4 predictors. To run diagnostics on the model, I generated a residual histogram, residual plot and qqplot.

Both qqplot and residual plot support the hypothesis that data is normally distributed while the histogram is heavily skewed and irregular with missing elements in the generated histogram.

QQPlot

Histogram of reisudals

Plotting the residuals

Does this support my assumption that data is normal

Abhi
  • 131
  • 3
  • 1
    What do you mean by "residual plot"? That could mean anything. When you say "qqplot", do you mean a qq plot of the sorted residuals vs expected normal quantiles? Anyway, if the residual histogram is heavily skewed, then the data appears not to be normal (or the regression model is inadequate). – Gordon Smyth Sep 23 '16 at 04:07
  • It would be easier to explain the discrepancy between histogram and QQ plot that you feel is there if we could see what you were looking at. Can you put the two plots in an image and post it? In any case you can't prove you have normality; at best you can show there's not strong evidence against it. – Glen_b Sep 23 '16 at 05:21
  • Check for a start: http://stats.stackexchange.com/questions/2492/is-normality-testing-essentially-useless – Tim Sep 23 '16 at 08:41
  • @Glen_b added the plots – Abhi Sep 24 '16 at 14:39
  • Please describe your original data . – IrishStat Sep 24 '16 at 20:50
  • Your data will not actually be drawn from a normal distribution. The important thing is whether it's reasonably close to normal or if it's non-normal in a way (and to an extent) that would seriously impact your inference. There's some indication of clumping in your residuals -- can you describe the original response variable? Is it discrete in some way? – Glen_b Sep 25 '16 at 10:49

2 Answers2

2

Departures from normality are generally a lot easier to spot on a qqplot than a histogram of the residuals. So, if your qqplot is good, and the histogram looks bad, this is likely just because you are over-reading random noise and arbitrary binning in the histogram (or, have made a mistake and are not comparing like with like).

Tim
  • 3,255
  • 14
  • 24
  • Yes. Now that we can see the histogram, it turns out to be not skew at all, so the problem appears to be too many bins for the histogram and over-interpretation of the right most observation. – Gordon Smyth Sep 28 '16 at 00:28
1

Use anderson-darling and cramer-von mises for normality test

ad.test(X)
cvm.test (X)

Nourhaine Nefzi
  • 53
  • 7
  • Chi-squared is another well worth mentioning, and any one test may not be optimal, so one should do several. – Carl Sep 23 '16 at 18:06
  • Chi-square is testing the distribution of the dataset. The formula, Χ2 = Σ [ (Or,c - Er,c)2 / Er,c ], is looking at the difference between observed value and mean. I am not able to get how it can be used to confirm normality of the dataset – Abhi Sep 24 '16 at 14:48
  • 1
    @Abhi you misunderstand what Carl is proposing but it doesn't matter because it's not a very useful suggestion -- the chi-square test is very low in power, so if you wanted to use a goodness of fit test you wouldn't use that one. On the other hand, I'd strongly advise you not to test goodness of fit. It makes sense to look at a display (since it's telling you something nearer to what you need to know), but a formal test will lead you to frequently reject a suitable model while leaving you unconcerned when there's more serious risk. – Glen_b Sep 25 '16 at 10:47