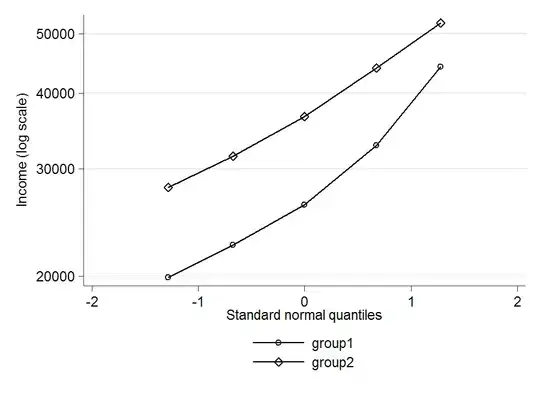
I have percentile data (P10, P25, P75 and P90) for a variable.
I also have the mean and median for each group:
group mean median P10 P25 P75 P90
1 30100 26200 19900 22500 32800 44200
2 38700 36600 28000 31500 44000 52100
How do I:
- Create a probability density function based on these variables.
- Use that function to give me the % in specific step intervals? (I.e. answering the question: How many out of 100 are in the 30000-31000 interval for group 2?)
Thanks.