Cool problem! As Xi'an's derivation shows, it is related to minimizing the KL-divergence from Q to P. Cliff provides some important context as well.
The problem can be solved trivially using optimization software, but I don't see a way to write a closed-form formula for the general solution. If $q_i \geq 0 $ never binds, then there is an intuitive formula.
Almost certainly optimal $\mathbf{q} \neq \mathbf{p}$ (though see my example graphs at the end, it might be close). And $\max \mathrm{E}[x]$ is not the same problem as $\max \mathrm{E}[\log(x)]$. Observe $x + y$ is not an equivalent objective as $\log(x) + \log(y)$. It's not a monotonic transformation. Expectation is a sum and the log goes inside the sum, so it's not a monotonic transformation of the objective function.
KKT conditions (i.e. necessary and sufficient conditions) for a solution:
Define $q_0 = 0$ and $q_{n+1} = 0$. The problem is:
\begin{equation}
\begin{array}{*2{>{\displaystyle}r}}
\mbox{maximize (over $q_i$)} & \sum_{i=1}^n p_i \log \left( q_{i-1} + q_i + q_{i+1} \right) \\
\mbox{subject to} & q_i \geq 0 \\ & \sum_{i=1}^n q_i = 1
\end{array}
\end{equation}
Lagrangian:
$$ \mathcal{L} = \sum_i p_i \log \left( q_{i-1} + q_i + q_{i+1} \right) + \sum_i \mu_i q_i -\lambda \left( \sum_i q_i - 1\right) $$
This is a convex optimization problem where Slater's condition holds therefore the KKT conditions are necessary and sufficient conditions for an optimum.
First order condition:
$$ \frac{p_{i-1}}{q_{i-2} + q_{i-1} + q_{i}} + \frac{p_i}{q_{i-1} + q_i + q_{i+1}} + \frac{p_{i+1}}{q_{i} + q_{i+1} + q_{i+2}} = \lambda - \mu_i $$
Complementary slackness:
$$\mu_i q_i = 0 $$
And of course $\mu_i \geq 0$. (It appears from my testing that $\lambda = 1$ but I don't immediately see why.) $\mu_i$ and $\lambda$ are Lagrange multipliers.
Solution if $q_i \geq 0$ never binds.
Then consider solution
$$ p_i = \frac{q_{i-1} + q_i + q_{i+1}}{3} \quad \quad \mu_i = 0 \quad \quad \lambda = 1$$
Plugging into the first order condition, we get $\frac{1}{3} + \frac{1}{3} + \frac{1}{3} = 1$. So it works (as long as $\sum_i q_i = 1$ and $q_i \geq 0$ are also satisfied).
How to write the problem with matrices:
Let $\mathbf{p}$ and $\mathbf{q}$ be vectors. Let $A$ be a tri-band diagonal matrix of ones. Eg. for $n = 5$
$$A = \left[\begin{array}{ccccc} 1 & 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0& 0 \\ 0 & 1 & 1 & 1 & 0 \\0 &0 & 1 & 1&1\\ 0 &0 &0 & 1 & 1 \end{array} \right] $$
Problem can be written with more matrix notation:
\begin{equation}
\begin{array}{*2{>{\displaystyle}r}}
\mbox{maximize (over $\mathbf{q}$)} & \mathbf{p}'\log\left(A \mathbf{q} \right) \\
\mbox{subject to} & q_i \geq 0 \\ & \sum_i q_i = 1
\end{array}
\end{equation}
This can be solved fast numerically but I don't see a way to a clean closed form solution?
Solution is characterized by:
$$A\mathbf{y} = \lambda - \mathbf{u} \quad \quad \mathbf{x} = A \mathbf{q} \quad \quad y_i = \frac{p_i}{x_i} $$
but I don't see how that's terribly helpful beyond checking your optimization software.
Code to solve it using CVX and MATLAB
A = eye(n) + diag(ones(n-1,1),1) + diag(ones(n-1,1),-1);
cvx_begin
variable q(n)
dual variable u;
dual variable l;
maximize(p'*log(A*q))
subject to:
u: q >= 0;
l: sum(q) <= 1;
cvx_end
Eg. inputs:
p = 0.0724 0.0383 0.0968 0.1040 0.1384 0.1657 0.0279 0.0856 0.2614 0.0095
has solution:
q = 0.0000 0.1929 0.0000 0.0341 0.3886 0.0000 0.0000 0.2865 0.0979 0.0000
Solution I get (blue) when I have a ton of bins basically following normal pdf (red):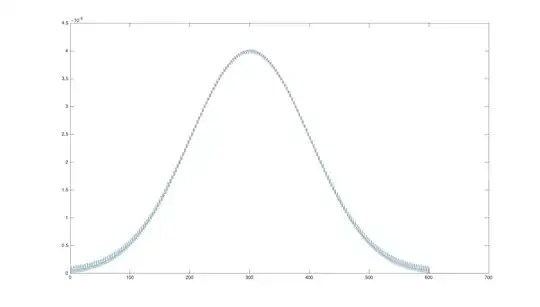 
Another more arbitrary problem:
Very loosely, for $p_{i-1} \approx p_i \approx p_{i+1}$ you get $q_i \approx p_i$, but if $p_i$ moves around a ton, you get some tricky stuff going on where the optimization tries to put the mass on $q_i$'s in the neighborhood of $p_i$ mass, strategically placing it between $p_i$'s with mass.
Another conceptual point is that uncertainty in your forecast will effectively smooth your estimate of $p$, and a smoother $p$ will have a solution $q$ that's closer to $p$. (I think that's right.)
