If you look at the wikipedia explanation of Metropolis adjusted Langevin Algorithm, the acceptance ratio is given by
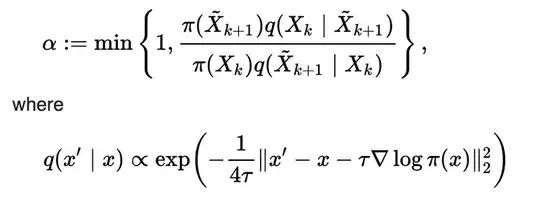
The second equation involves taking the gradient of the log of $\pi(x)$. However, the whole reason for doing MCMC is that you do not know the exact formula for $\pi(x)$, only within a multiplicative constant. That's why take the ratio as shown in the 1st equation is ok.
So how do you implement MALA given this limitation?
If you know $\pi(\cdot)$ up to a constant, a requirement for Metropolis-Hastings algorithms, the gradient $$\nabla \log \pi(\cdot)$$is also independent from this constant.
Expanding on Xi'an's answer, if $\pi(x) = c f(x)$, where $c$ is the unknown normalizing constant, then \begin{align*} \pi(x) & = c f(x)\\ \log \pi(x) & = \log(c) + \log f(x)\\ \Delta\log \pi(x) &= \Delta \log f(x). \end{align*}
Thus, the normalizing constant is not required.
