I want to use deep learning in my project. I went through a couple of papers and a question occurred to me: is there any difference between convolution neural network and deep learning? Are these things the same or do they have any major differences, and which is better?
- 556
- 2
- 18
- 733
- 3
- 9
- 14
-
Tell me what is exact difference from deep learning and convolutional neural network I am some what confusion at these 2 topics – Yamini May 04 '19 at 07:52
5 Answers
Deep Learning is the branch of Machine Learning based on Deep Neural Networks (DNNs), meaning neural networks with at the very least 3 or 4 layers (including the input and output layers). But for some people (especially non-technical), any neural net qualifies as Deep Learning, regardless of its depth. And others consider a 10-layer neural net as shallow.
Convolutional Neural Networks (CNNs) are one of the most popular neural network architectures. They are extremely successful at image processing, but also for many other tasks (such as speech recognition, natural language processing, and more). The state of the art CNNs are pretty deep (dozens of layers at least), so they are part of Deep Learning. But you can build a shallow CNN for a simple task, in which case it's not (really) Deep Learning.
But CNNs are not alone, there are many other neural network architectures out there, including Recurrent Neural Networks (RNN), Autoencoders, Transformers, Deep Belief Nets (DBN = a stack of Restricted Boltzmann Machines, RBM), and more. They can be shallow or deep. Note: even shallow RNNs can be considered part of Deep Learning since training them requires unrolling them through time, resulting in a deep net.
- 1,930
- 3
- 16
- 29
-
@MiniQurak. Please correct me i am wrong. what I understand is CNN is just one the architectures of deep nets just like Autoencoders, Deep Belief Nets, Recurrent Neural Networks (RNN).. is it correct? – Aadnan Farooq A Sep 14 '16 at 08:13
-
-
then can we can say which architecture is better depending on the dataset? or what are the key factors? – Aadnan Farooq A Sep 14 '16 at 08:32
-
2CNNs are great for image recognition tasks. They also shine whenever the data has some form of hierarchical structure, with local patterns (eg. line segments) assembled into large patterns (eg. squares, triangles), assembled into larger patterns (eg. house, plane). This works well for speech recognition tasks. RNNs are great for time series (eg. predicting the weather), and generally handling sequences of data (eg. sentences). They are used a lot for NLP (natural language processing). AutoEncoders are unsupervised, they learn patterns in the data. – MiniQuark Sep 14 '16 at 08:40
-
Are autoencoders necessarily deep? I thought their defining property was that they approximated their input as output via _at least one_ hidden layer narrower than the input, but that could be the single hidden layer. – MSalters Sep 14 '16 at 08:47
-
I have seen many papers that used CNN for the resolution enhancement of the satellite images. That's why I am curious that why it's not possible to use other architecture for that . – Aadnan Farooq A Sep 14 '16 at 08:51
-
In theory you could use a deep neural network with many fully connected layers, but (1) it would have way too many parameters, and (2) it would be incredibly long to train. CNNs solve this by only partially connecting consecutive layers. Imagine 300x200 pixel images: thats 60,000 pixels. Imagine that your first layer has 1,000 neurons. If it's a fully connected layer, you now have 60 millions weights, just for the first layer. That said, it is possible to classify small images using other network architectures than CNNs. – MiniQuark Sep 14 '16 at 15:08
-
For example, the following code classifies MNIST images (28x28 pixels) using an RNN that looks at one row at a time: https://github.com/aymericdamien/TensorFlow-Examples/blob/master/examples/3_NeuralNetworks/recurrent_network.py – MiniQuark Sep 14 '16 at 15:09
-
@Firebug Thanks for your feedback, I updated my answer to make that clearer. – MiniQuark May 04 '19 at 11:29
-
1
Within the fields of adaptive signal processing / machine learning, deep learning (DL) is a particular methodology in which we can train machines complex representations.
Generally, they will have a formulation that can map your input $\mathbf{x}$, all the way to the target objective, $\mathbf{y}$, via a series of hierarchically stacked (this is where the 'deep' comes from) operations. Those operations are typically linear operations/projections ($W_i$), followed by a non-linearities ($f_i$), like so:
$$ \mathbf{y} = f_N(...f_2(f_1(\mathbf{x}^T\mathbf{W}_1)\mathbf{W}_2)...\mathbf{W}_N) $$
Now within DL, there are many different architectures: One such architecture is known as a convolutional neural net (CNN). Another architecture is known as a multi-layer perceptron, (MLP), etc. Different architectures lend themselves to solving different types of problems.
An MLP is perhaps one of the most traditional types of DL architectures one may find, and that's when every element of a previous layer, is connected to every element of the next layer. It looks like this:
In MLPs, the matricies $\mathbf{W}_i$ encode the transformation from one layer to another. (Via a matrix multiply). For example, if you have 10 neurons in one layer connected to 20 neurons of the next, then you will have a matrix $\mathbf{W} \in R^{10 \text{x} 20}$, that will map an input $\mathbf{v} \in R^{10 \text{x} 1}$ to an output $\mathbf{u} \in R^{1 \text{x} 20}$, via: $\mathbf{u} = \mathbf{v}^T \mathbf{W}$. Every column in $\mathbf{W}$, encodes all the edges going from all the elements of a layer, to one of the elements of the next layer.
MLPs fell out of favor then, in part because they were hard to train. While there are many reasons for that hardship, one of them was also because their dense connections didnt allow them to scale easily for various computer vision problems. In other words, they did not have translation-equivariance baked in. This meant that if there was a signal in one part of the image that they needed to be sensitive to, they would need to re-learn how to be sensitive to it if that signal moved around. This wasted the capacity of the net, and so training became hard.
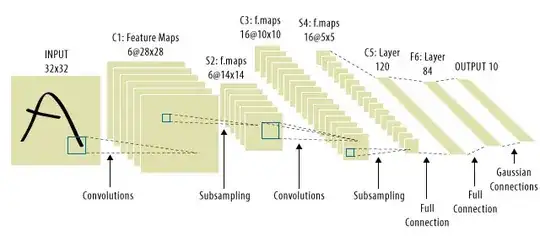
This is where CNNs came in! Here is what one looks like:
CNNs solved the signal-translation problem, because they would convolve each input signal with a detector, (kernel), and thus be sensitive to the same feature, but this time everywhere. In that case, our equation still looks the same, but the weight matricies $\mathbf{W_i}$ are actually convolutional toeplitz matricies. The math is the same though.
It is common to see "CNNs" refer to nets where we have convolutional layers throughout the net, and MLPs at the very end, so that is one caveat to be aware of.
- 132,789
- 81
- 357
- 650
- 759
- 4
- 7
-
1
-
@MiniQuark Thanks! Yes - you can write out a convolution as a multiplication by a toeplitz matrix. :) – Tarin Ziyaee Sep 16 '16 at 18:29
-
@TarinZiyaee and MiniQurak Can you guys please suggest me any good book/journal article/tutorial for the beginner to learn about the Deep learning in detail. – Aadnan Farooq A Sep 20 '16 at 02:18
-
Deep learning = deep artificial neural networks + other kind of deep models.
Deep artificial neural networks = artificial neural networks with more than 1 layer. (see minimum number of layers in a deep neural network or Wikipedia for more debate…)
Convolution Neural Network = A type of artificial neural networks
- 42,093
- 30
- 155
- 271
-
Fair enough, Deep Learning also includes "Multilayer kernel machines", and CNNs can be shallow. :) – MiniQuark Sep 14 '16 at 19:01
-
-
artificial neural networks with more than 1 layer..... I'm not sure a network with just 2 layers is called a deep network. – SmallChess Sep 16 '16 at 05:29
-
1@StudentT Maybe, I don't work in marketing ;) https://en.wikipedia.org/w/index.php?title=Deep_learning&oldid=739575646#Definitions – Franck Dernoncourt Sep 16 '16 at 15:08
-
1This should be the top answer, because CNNs are not necessarily deep, and Deep learning is not only about ANNs (in the ordinary sense). – Firebug Sep 27 '18 at 13:08
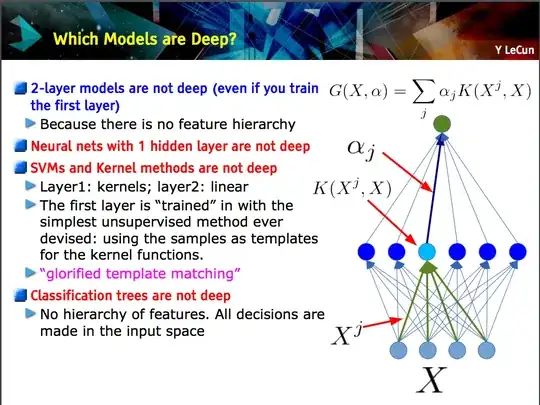
This slide by Yann LeCun makes the point that only models with a feature hierarchy (lower-level features are learned at one layer of a model, and then those features are combined at the next level) are deep.
A CNN can be deep or shallow; which is the case depends on whether it follows this "feature hierarchy" construction because certain neural networks, including 2-layer models, are not deep.
- 76,417
- 20
- 189
- 313
Deep learning is a general term for dealing with a complicated neural network with multiple layers. There is no standard definition of what exactly is deep. Usually, you can think a deep network is something that is too big for your laptop and PC to train. The data set would be so huge that you can't fit it into your memory. You might need GPU to speed up your training.
Deep is more like a marketing term to make something sounds more professional than otherwise.
CNN is a type of deep neural network, and there are many other types. CNNs are popular because they have very useful applications to image recognition.
- 1,930
- 3
- 16
- 29
- 6,764
- 4
- 27
- 48
-
I would like to kindly object to a few of these statements: a network is generally considered deep when it has more than one hidden layer, and most people would agree that having more than 10 hidden layers is definitely deep. It is quite possible to train deep networks on your laptop, I do it all the time. The dataset does not *have* to be huge, in particular if you use transfer learning (ie. reuse layers from a pretrained network), and/or data augmentation. There is certainly a lot of hype around the word "deep", but there are dedicated techniques for deep learning so it's not just hype. :) – MiniQuark Sep 16 '16 at 14:58
-
@MiniQuark With data augmentation, your data set will still be large, just that you start off with something small... – SmallChess Sep 16 '16 at 15:01
-
Good point, you're right. What I meant to say is that the dataset would fit in memory since you would generate most of the data on the fly. – MiniQuark Sep 16 '16 at 15:03