I do not know what method is appropriate to fit (say, a Log-Normal distribution) over an observed distribution. I say observed to make it sound generic because I am not sure if this qualifies as an Empirical distribution.
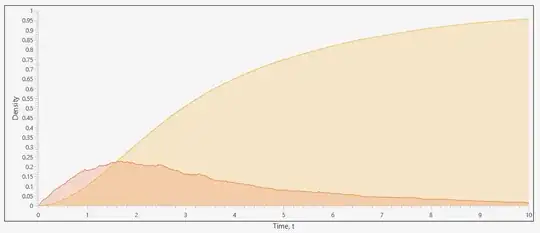
Anyways, after my simulation the data looks as follows:
Note that the density is very choppy but the CDF is much more smoother.
I would very much appreciate some advise how to approach this problem. I am looking for a method name, or some sort of sudo code. (I have to use Java to code it but that is not too important)