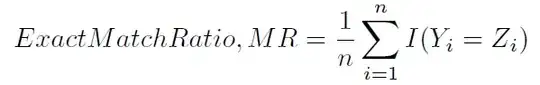Multilabel classification metrics on scikit

Question

I am trying to build a multi-label classifier so as to assign topics to existing documents using scikit

I am processing my documents passing them through the TfidfVectorizer the labels through the MultiLabelBinarizer and created a OneVsRestClassifier with an SGDClassifier as the estimator.

However when testing my classifier I only get scores up to .29 which from what I've read is pretty low for similar problems. I tried multiple options on the TfidfVectorizer such as stopwords, unigrams, stemming and nothing seems to change the result that much.

I've also used GridSearchCV to get the best parameters for my estimator and currently I am out of ideas on what to try next.

At the same time, from what I understand I cannot use scikit.metrics with OneVsRestClassifier so how can I get some metrics (F1,Precision,Recall etc) so as to figure out what is wrong?

Could it be a problem with my data corpus?

Update: I've also tried using CountVectorizer and HashingVectorizer and pipelining them to TfidfTransformer but the results are similar. So I am guessing that the bag-of-words approach is doing it's best in the tokenisation domain and the rest is up to the classifier...

Answer 1

The subset accuracy is indeed a harsh metric. To get a sense of how good or bad 0.29 is, some idea:

• look at how many labels you have an average for each sample
• look at the inter-annotator agreement, if available (if not, try yourself to see what subset accuracy the obtained when you are the classifier)
• think whether topic are well defined
• look at how many samples you have for each label

You may also want to compute the hamming score, to see whether your classifier is clueless, or is instead decently good but have issue predicting all labels correctly. See below to compute the hamming score.

At the same time, from what I understand I cannot use scikit.metrics with OneVsRestClassifier so how can I get some metrics (F1,Precision,Recall etc) so as to figure out what is wrong?

See How to compute precision/recall for multiclass-multilabel classification?. I forgot whether sklearn supports it, I recall it had some limitations, e.g. sklearn doesn't support multi-label for confusion matrix. That would be a good idea to see these numbers indeed.

---

Hamming score:

In a multilabel classification setting, sklearn.metrics.accuracy_score only computes the subset accuracy (3): i.e. the set of labels predicted for a sample must exactly match the corresponding set of labels in y_true.

This way of computing the accuracy is sometime named, perhaps less ambiguously, exact match ratio (1):

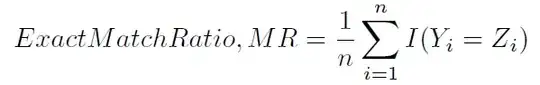
Another typical way to compute the accuracy is defined in (1) and (2), and less ambiguously referred to as the Hamming score (4) (since it is closely related to the Hamming loss), or label-based accuracy). It is computed as follows:

Here is a python method to compute the Hamming score:

# Code by https://stackoverflow.com/users/1953100/william
# Source: https://stackoverflow.com/a/32239764/395857
# License: cc by-sa 3.0 with attribution required

import numpy as np

y_true = np.array([[0,1,0],
                   [0,1,1],
                   [1,0,1],
                   [0,0,1]])

y_pred = np.array([[0,1,1],
                   [0,1,1],
                   [0,1,0],
                   [0,0,0]])

def hamming_score(y_true, y_pred, normalize=True, sample_weight=None):
    '''
    Compute the Hamming score (a.k.a. label-based accuracy) for the multi-label case
    https://stackoverflow.com/q/32239577/395857
    '''
    acc_list = []
    for i in range(y_true.shape[0]):
        set_true = set( np.where(y_true[i])[0] )
        set_pred = set( np.where(y_pred[i])[0] )
        #print('\nset_true: {0}'.format(set_true))
        #print('set_pred: {0}'.format(set_pred))
        tmp_a = None
        if len(set_true) == 0 and len(set_pred) == 0:
            tmp_a = 1
        else:
            tmp_a = len(set_true.intersection(set_pred))/\
                    float( len(set_true.union(set_pred)) )
        #print('tmp_a: {0}'.format(tmp_a))
        acc_list.append(tmp_a)
    return np.mean(acc_list)

if __name__ == "__main__":
    print('Hamming score: {0}'.format(hamming_score(y_true, y_pred))) # 0.375 (= (0.5+1+0+0)/4)

    # For comparison sake:
    import sklearn.metrics

    # Subset accuracy
    # 0.25 (= 0+1+0+0 / 4) --> 1 if the prediction for one sample fully matches the gold. 0 otherwise.
    print('Subset accuracy: {0}'.format(sklearn.metrics.accuracy_score(y_true, y_pred, normalize=True, sample_weight=None)))

    # Hamming loss (smaller is better)
    # $$ \text{HammingLoss}(x_i, y_i) = \frac{1}{|D|} \sum_{i=1}^{|D|} \frac{xor(x_i, y_i)}{|L|}, $$
    # where
    #  - \\(|D|\\) is the number of samples  
    #  - \\(|L|\\) is the number of labels  
    #  - \\(y_i\\) is the ground truth  
    #  - \\(x_i\\)  is the prediction.  
    # 0.416666666667 (= (1+0+3+1) / (3*4) )
    print('Hamming loss: {0}'.format(sklearn.metrics.hamming_loss(y_true, y_pred))) 

Outputs:

Hamming score: 0.375
Subset accuracy: 0.25
Hamming loss: 0.416666666667

---

(1) Sorower, Mohammad S. "A literature survey on algorithms for multi-label learning." Oregon State University, Corvallis (2010).

(2) Tsoumakas, Grigorios, and Ioannis Katakis. "Multi-label classification: An overview." Dept. of Informatics, Aristotle University of Thessaloniki, Greece (2006).

(3) Ghamrawi, Nadia, and Andrew McCallum. "Collective multi-label classification." Proceedings of the 14th ACM international conference on Information and knowledge management. ACM, 2005.

(4) Godbole, Shantanu, and Sunita Sarawagi. "Discriminative methods for multi-labeled classification." Advances in Knowledge Discovery and Data Mining. Springer Berlin Heidelberg, 2004. 22-30.

Answer 2

The Hamming-Loss and Exact match (also called subset accuracy) can be calculated Using Scikit-learn as follows.

import numpy as np
from sklearn.metrics import hamming_loss, accuracy_score 
y_true = np.array([[0,1,0],
                   [0,1,1],
                   [1,0,1],
                   [0,0,1]])

y_pred = np.array([[0,1,1],
                   [0,1,1],
                   [0,1,0],
                   [0,0,0]])

print("accuracy_score:", accuracy_score(y_true, y_pred))
print("Hamming_loss:", hamming_loss(y_true, y_pred))

Output

accuracy_score: 0.25
Hamming_loss: 0.4166666666666667

Answer 3

Is the 0.29 score not enough? What does your confusion matrix look like? Are there some topics that cannot be separated out maybe by only looking at the word contents?

Otherwise, try to turn your problem around: Hypothesise that the low scores is actually the best your classifier can do on your data. That would mean that your documents are not classifiable using this approach.

To test this hypothesis, you need a set of test documents with known bag-of-word characteristics (which you create yourself). You should get 100% scores.

If you do not, then you have a bug. Otherwise, you need a different approach to classify your documents. Ask yourself: how do the documents from the different classes differ from one another? Do I need to look at other features of my documents, etc.

Answer 4

The following is a vectorized version of the Hamming score:

import numpy as np


def hamming_score(pred, answer):
    out = ((pred & answer).sum(axis=1) / (pred | answer).sum(axis=1)).mean()
    if np.isinf(out):
        out = np.array(1.0)
    return out


pred = np.array([[0, 1, 1], [0, 1, 1], [0, 1, 0], [0, 0, 0]])
answer = np.array([[0, 1, 0], [0, 1, 1], [1, 0, 1], [0, 0, 1]])

hamming_score(pred, answer)

or in PyTorch

import torch


def hamming_score(pred, answer):
    out = ((pred & answer).sum(dim=1) / (pred | answer).sum(dim=1)).mean()
    if out.isnan():
        out = torch.tensor(1.0)
    return out

answer = torch.tensor([[0, 1, 0], [0, 1, 1], [1, 0, 1], [0, 0, 1]])
pred = torch.tensor([[0, 1, 1], [0, 1, 1], [0, 1, 0], [0, 0, 0]])

hamming_score(pred, answer)