3

I have paired data, but repeated observations, which make the data to be paired with dependent observations. I read Wilcoxon signed rank test assumes the observations are independent.

Which test can I use if the data contains dependent observations, repeated by groups of 5? This is, the first data points are from a repeated observation, the second 5 from another repeated observation, and so on. Is Wilcoxon ok for this kind of data anyway?

For example, in the data below, where the same dataset was processed with two different programming languages, having dependent data but not independent observations. My confusion is, Wilcoxon seems to be correct to use here, only if my data was not replicated. Am I right? Which test should I use with dependent samples and dependent observations?

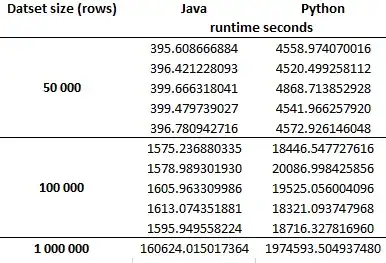
enter image description here

User2130
  • 177
  • 2
  • 12
  • 1
    I don't follow your situation / data setup. Can you say more about your study, your data, & what you are trying to achieve? Can you provide some sample data? – gung - Reinstate Monica Sep 03 '16 at 17:16

3 Answers3

6

You can think of your data as blocked, or being a two-factor experiment where one factor is a nuisance. These are repeated measures, but they are not paired because the blocks aren't of size $2$. Taking, for example, the data that come from the java code run on a given dataset of 50,000, you have $5$ repeated measures. These are matched to another $5$ repeated measures from the Python code, in the sense that the codes were run on the same dataset. A matched pair would be $1$ datum that corresponds to $1$ datum. You have $5$ data that correspond to $5$ data. Two matched sets of size $5$ each aren't a 'pair'.

In theory, you could use a random effect to account for the non-independence of the data. However, with just three datasets, this is pretty sketchy. In your case, I would control for the non-independence with a fixed factor. In other words, you have two factors in your experiment, one of which (dataset) you don't really care about and only want to control for to account for the non-independence that would otherwise occur.

The question of whether you should make parametric assumptions (like normality) is well addressed in this great CV thread: How to choose between t-test or non-parametric test e.g. Wilcoxon in small samples. If you wanted to use a nonparametric approach, you could use an ordinal logistic regression (cf., What is the non-parametric equivalent of a two-way ANOVA that can include interactions?). If you wanted the parametric equivalent, you could run a standard two-way ANOVA. The ordinal model is probably safer, but it won't matter with your data either way, since the effect is so large.

On a different note, let me address some of the misunderstandings in the question. There are two tests that are sometimes called 'the Wilcoxon test': the Wilcoxon rank sum test, and the Wilcoxon signed rank test. The former is for two independent samples, and is also called the Mann-Whitney U-test. The latter is for two dependent samples. Neither requires that your data are normally distributed. If your data were paired (e.g., if you ran each dataset only once with each software), then you could use the Wilcoxon signed rank test. The complication here is that you don't have paired data.

gung - Reinstate Monica
  • 132,789
  • 81
  • 357
  • 650
  • Ok I see. I understand I do not have pairs, but still I have dependent samples, with dependent observations if I am not wrong. With dependent samples I cannot use t-test, with dependent observations I cannot use Wilcoxon. What should I do? – User2130 Sep 03 '16 at 18:48
  • You can account for the dependence by using a fixed effect for dataset / dataset size. That is, you would fit a two-way model in which you don't care about the 2nd (dataset) factor. @SparkGeek – gung - Reinstate Monica Sep 03 '16 at 18:54
  • I am really sorry, I don't think I understand the comment. :( Does that mean if I test only the first 5 data points, that counts as independent observations? – User2130 Sep 03 '16 at 19:02
  • @SparkGeek, no. You test all 22 data as a function of 2 factors. Eg, if you used R, you could use `library(rms); orm(Y~dataset+software)`, or `anova(lm(Y~dataset+software))`. – gung - Reinstate Monica Sep 03 '16 at 19:29
  • Your last edition helps me greatly. I actually have another samples with 5 runs each dataset, so I use Friedman's test, it helps me a lot that you confirm it's ok. But I use it when comparing another three programming languages (three-samples model). Would that be ok to use Friedman's with two samples? and ignore the last dataset with 1 run? – User2130 Sep 03 '16 at 19:48
  • @SparkGeek, on 2nd thought, scratch that comment about Friedman's test. I think you need 1 run of each dataset for each software for FT. – gung - Reinstate Monica Sep 03 '16 at 19:52
  • Friedman's test on MatLab has a "reps" parameter, that allows me to fix "5" so it knows that in the column there are replicates. – User2130 Sep 03 '16 at 19:57
  • From [Friedman's definition](https://en.wikipedia.org/wiki/Friedman_test): "Similar to the parametric repeated measures ANOVA, it is used to detect differences in treatments across multiple test attempts." I am actually looking for something like this but for two samples, like the equivalent of Friedman's test, valid for two samples, or to know if I can use it with two samples. – User2130 Sep 03 '16 at 20:01
  • I'm not sure, @SparkGeek, you could ask a new question. Friedman's test is prototypically where each unit is measured in each of several conditions, but could also be several measurements over time w/i a single condition. For your data, using the dataset as a fixed effect in a two-way design will be fine. – gung - Reinstate Monica Sep 03 '16 at 21:56
2

There's no need for any hypothesis testing here. You can see that there's a significant magnitude difference between the Java and Python performance.

user_1177868
  • 712
  • 4
  • 13
  • I'm getting crazy :( . I put this as an example, to notice the model. I would skip hypothesis testing on the treatments that contain a significant magnitude difference, as I have been properly advised. :) But then the issue is that I got a dependent two-samples, with dependent observations. Wilcoxon needs observations to be independent, then I don't what to do in that case. – User2130 Sep 03 '16 at 19:38
  • That's clearly true, but it's certainly a reasonable question for the OP to want to know what the correct procedure would be for this case. – gung - Reinstate Monica Sep 03 '16 at 19:40
0

Here, I assume you're interested in the difference between Java and Python in terms of execution time. I think you should consider paired t-test for each block (data size).

  • You have paired data (your sample with Java and the same sample with Python)
  • Each pair is correlated because you use the same machine to do the test (I assume it's the same machine)
  • The execution time can certainly be approximated by normal
  • Your data is blocked by the data size (which is a covariate)

If you want to include all data into a single model, you'll need to use ANCOVA one-way repeated measure.

PS: It's not essential to do statistical testing here because you know the results will be significant and the p-value will be very small.

EDIT @gung doesn't believe your data is paired even you say so. If you don't believe the data is paired, independent t-test and ANCOVA will be good.

User2130
  • 177
  • 2
  • 12
SmallChess
  • 6,764
  • 4
  • 27
  • 48
  • There are multiple data from each source that are matched, not just 2 (a pair). It does not appear that a paired test (t, Wilcoxon, etc) would be appropriate here. – gung - Reinstate Monica Sep 03 '16 at 18:08
  • @gung There're only two sources, Python and Java. We measure repeatedly on those two sources (population). – SmallChess Sep 03 '16 at 18:10
  • @gung I see it like a single categorical independent variable (programming language) with two groups (Java and Python). if we had C++, that would require one-way repeated measure. What do you think? – SmallChess Sep 03 '16 at 18:11
  • From, eg, `java` & `50k`, you have 5 data / repeated measures. Those 5 are matched to 5 data from `Python`. These are not 'paired'. – gung - Reinstate Monica Sep 03 '16 at 18:11
  • @gung I think they are paired because they are done by the same machine under slightly different conditions. – SmallChess Sep 03 '16 at 18:13
  • @gung Time is a common factor to make "paired" observation, but Java+Python can also be a paired factor. If Java and Python are really the same thing, the difference will be just noise. – SmallChess Sep 03 '16 at 18:15
  • A [pair](http://www.dictionary.com/browse/pairs) is "two identical, similar, or corresponding things that are matched for use together". That is not what you have here. You have *two **sets of 5** identical, similar, or corresponding things that are matched for use together*. – gung - Reinstate Monica Sep 03 '16 at 18:16
  • It's paired because the same dataset is applied on the two, in the same machine. I am not sure about the normality of my samples, and I read with small data points I should use a non-parametric test. What do you think? Is there a way to do hypothesis testing with non-parametric, paired data but dependent observations? – User2130 Sep 03 '16 at 18:20
  • @SparkGeek Within each block (data size), your data is certainly normal and a parametric test is better. Why would you want to lose statistical power with non-parametric test? – SmallChess Sep 03 '16 at 18:21
  • Because when applying lilliefors test I got a results indicating I cannot reject H0. :( – User2130 Sep 03 '16 at 18:23
  • And also because I have few data points. I read when the data points are not many, it is preferable to use a non-parametrical test. My main concern are the dependable observations. Most of the tests assume independent observations. I am not sure if even it exist some test for dependent observations, I was thinking in something like Friedman's test but for two samples. – User2130 Sep 03 '16 at 18:39