I have the following question at hand:
Suppose $U,V$ are iid random variables following Unif$(0,1)$. what is the conditional distribution of $U$ given $Z:=\max(U,V)$ ?
I tried writing $Z=\Bbb{I}\cdot V+(1-\Bbb{I})\cdot U$ where $\Bbb{I}=\begin{cases}1&U<V\\0&U>V\end{cases}$
But I am not getting anywhere.
A picture might help. Independent uniform distributions on the interval $[0,1]$ may be considered a uniform distribution on the unit square $I^2 = [0,1]\times [0,1]$. Events are regions in the square and their probabilities are their areas.
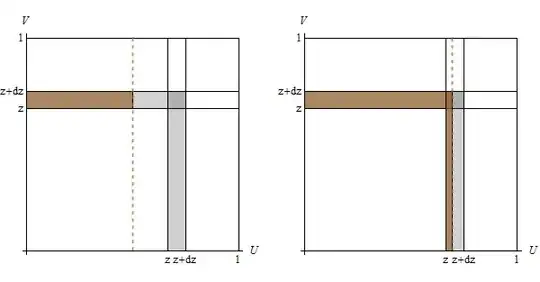
Let $z$ be any possible value of $\max(U,V)$. The set of coordinates $(U,V)$ where $\max(U,V)=z$ forms the top and right edges of a square of side $z$. Let $dz$ be a small positive number. The set of coordinates $(U,V)$ whose maximum lies between $z$ and $z+dz$ forms a narrow thickening of that square, as shaded in the figure. Its area is the difference of the areas of two squares, one of side $z+dz$ and the other of side $z$, whence
$$\Pr(z \le Z \le z+dz) = (z+dz)^2 - z^2 = 2z\,dz + (dz)^2.\tag{1}$$
Let $u$ be any possible value of $U$: it is marked with a vertical dashed line in the figures.
The left panel shows a case where $u \le z$: The chance that $U\le u$ would be the area to the left of that line (equal to $u$); but the event that $U\le u$ and $Z$ lies between $z$ and $z+dz$ is just the brown shaded area. It's a rectangle, so its area is its width $u$ times its height $dz$. Thus,
$$\Pr(U \le u, z \le Z \le z+dz) = u\,dz.\tag{2}$$
The right panel shows a case where $z \lt u \le z+dz$. Now the chance that $U \le u$ and $z \lt Z \le z+dz$ consists of two rectangles. The top one has base $u$ and height $dz$; the right one has base $(u-z)$ and height $z+dz$. Therefore
$$\Pr(U \le u, z \le Z \le z+dz) = u\, dz + (u-z)(z+dz).\tag{3}$$
By definition, the conditional probabilities are these chances divided by the total chance that $z \le Z \le z+dz$, given in $(1)$ above. Divide $(2)$ and $(3)$ by this value. Letting $dz$ be infinitesimal, and retaining the standard part of the result, gives the chances conditional on $Z=z$. Thus, when $0 \le u \le z$,
$$\Pr(U \le u\,|\, Z=z) = \frac{u\,dz}{2z\,dz + (dz)^2} = \frac{u}{2z + dz} \approx \frac{u}{2z}.$$
When $z \lt u \le z+dz$, write $u = z + \lambda dz$ for $0 \lt \lambda \le 1$ and compute
$$\Pr(U \le u|Z=z) = \frac{u\, dz + (u-z)(z+dz)}{2z\,dz + (dz)^2} = \frac{(z + \lambda dz)dz + (\lambda dz)(z+dz)}{2z\,dz+(dz)^2}\approx\frac{1+\lambda}{2}.$$
Finally, for $u \gt z+dz$, the brown area in the right panel has grown to equal the gray area, whence their ratio is $1$.
These results show that the conditional probability grows linearly from $0$ to $z/(2z)=1/2$ as $u$ grows from $0$ to $z$, then shoots up linearly from $1/2$ to $1$ in the infinitesimal interval between $z$ and $z+dz$, then stays at $1$ for all larger $u$. Here's a graph:
Because $dz$ is infinitesimal, it is no longer possible to distinguish $z$ from $z+dz$ visually: the plot jumps from a height of $1/2$ to $1$.
Putting the foregoing together into a single formula to be applied to any $z$ for which $0 \lt z \le 1$, we could write the conditional distribution function as
$$F_{U|Z=z}(u) = \left\{\begin{array}{ll} 0 & u \le 0 \\ \frac{u}{2z} & 0 \lt u\le z \\ 1 & u \gt z. \end{array} \right.$$
This is a complete and rigorous answer. The jump shows that a probability density function will not adequately describe the conditional distribution at the value $U=z$. At all other points, though, there is a density $f_{U|Z=z}(u)$. It is equal to $0$ for $u\le 0$, $1/(2z)$ for $0 \le u \lt z$ (the derivative of $u/(2z)$ with respect to $u$), and $0$ for $u \gt z$. You could use a "generalized function" to write this in a density-like form. Let $\delta_z$ be the "generalized density" giving a jump of magnitude $1$ at $z$: that is, it's the "density" of an atom of unit probability located at $z$. Then the generalized density at $z$ can be written $\frac{1}{2}\delta_z$ to express the fact that a probability of $1/2$ is concentrated at $z$. In full, we could write
$$f_{U|Z=z}(u) = \left\{\begin{array}{ll} 0 & u \le 0 \\ \frac{1}{2z} & 0 \lt u\lt z \\ \frac{1}{2}\delta_z(u) & u=z \\ 0 & u \gt z. \end{array} \right.$$
First consider the distribution of the maximum $Z$ conditional on $U=u$. The maximum $Z$ becomes equal to $u$ in the event that $V<u$ with conditional probability $u$. Otherwise, $Z$ takes some value greater than $u$ equal to $V$. The overall conditional distribution will thus be a mixture between a point mass at $u$ (of size u) and a uniform density on $(u,1)$ (integrating to $1-u$). Representing the point mass by the Dirac delta function, the generalised probability density function (gpdf) of this conditional distribution is $$ f_{Z|U=u}(z) = u\delta(z-u) + \begin{cases} 1 & \text{for }u<z<1 \\ 0 &\text{otherwise}. \end{cases} $$ The joint gpdf of $Z$ and $U$ is then \begin{align} f_{Z,U}(z,u) &= f_{Z|U=u}(z)f_U(u) \\ &= u\delta(z-u) + \begin{cases} 1 & \text{for }0<u<z<1 \\ 0 &\text{otherwise}. \end{cases} \end{align} The pdf of the maximum is $f_Z(z)=2z$. Hence, the conditional gpdf of $U$ given the maximum $Z$ becomes \begin{align} f_{U|Z=z}(u) &= \frac{f_{Z,U}(z,u)}{f_Z(z)} \\ &= \frac12\delta(z-u) + \begin{cases} \frac1{2z} & \text{for }0<u<z \\ 0 &\text{otherwise}, \end{cases} \end{align} a mixture between a point mass at $z$ with probability 1/2 and a uniform density on $(0,z)$ integrating to 1/2.
