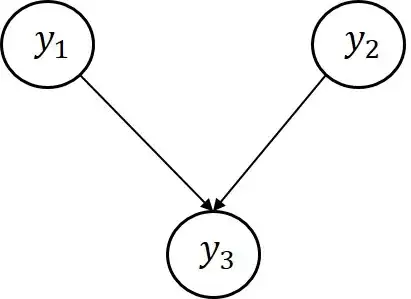
Optimizing the full likelihood function is sometimes time consuming and contains a lot of numerical issues and instabilities especially when matrix inversion is needed. If we have 3 input vectors $\boldsymbol{y}_{1},\boldsymbol{y}_{2},\boldsymbol{y}_{3}$ let $\mathbf{y}=[\boldsymbol{y}_{1},\boldsymbol{y}_{2},\boldsymbol{y}_{3}]$. Based on this, I want to model $\mathbf{y}$ $$ \mathbf{y}\sim N(0,K)$$ where K is a joint covariance matrix between all three input vectors. The Inputs are connected as shown in the figure below: $\boldsymbol{y}_{1}$ and $\boldsymbol{y}_{2}$ are independent while both $\boldsymbol{y}_{1}$ and $\boldsymbol{y}_{2}$ depend on $\boldsymbol{y}_{3}$. In other words the covariance matrix $K$ is expressed as follows $$K=\begin{pmatrix} k_{11} & 0 & k_{13}\\ 0& k_{22} & k_{23} \\ k_{13} & k_{23} & k_{33} \end{pmatrix}$$ Where $k$ is any postive semidefinite covariance function. Is there any specific way for me to exploit this independence and factorize the full likelihood function for example can I write $$f(\boldsymbol{y}_{1},\boldsymbol{y}_{2},\boldsymbol{y}_{3})=f(\boldsymbol{y}_{3}|\boldsymbol{y}_{1},\boldsymbol{y}_{2})*f(\boldsymbol{y}_{1})*f(\boldsymbol{y}_{2})$$ and optimize each part seprately? and what is the expression of $f(\boldsymbol{y}_{3}|\boldsymbol{y}_{1},\boldsymbol{y}_{2})$ given the covariance matrix above. Also is there a specific way I can use a composite likelihood approach such as a pairwise likelihood method.
Any good references on such normal likelihood factorizations is greatly appreciated