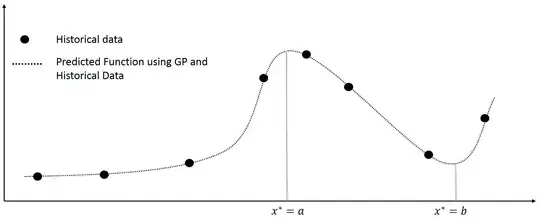
A Gaussian process (GP) is defined as a collection of random variables with a joint Gaussian distribution (Rasmussen 2006). It is well known that given observations $\left \{ \mathbf{x},\mathbf{y}\right\}$ and given a covariance function such as the squared exponential $$k(x,x^{'})= \sigma exp(-(x-x^{'})^{2}/l^{2})$$ then for any new input point $x^{*}$ , the response $y^{*}$ can be calculated based on the multivaraite normal theory as follows $$\\\begin{pmatrix} \mathbf{y}\\y^{*} \end{pmatrix} \sim N(\mathbf{0},\begin{bmatrix} K & K_{*}^{T} \\ K_{*} & K_{**} \end{bmatrix})\\y^{*}|\mathbf{y} \sim N(K_{*}K^{-1}\mathbf{y},K_{**}-K_{*}K^{-1}K_{*}^{T}) $$ I want to find the input points relating to the maximum and minimum prediction response over a domain of interest $x\in D$ , for instance in the figure below I want to find the input points $x^{*}=a,x^{*}=b$
 What are the best and most efficient techniques that can be utilizaed for the gaussain process. Specifically, I am looking for possibly utilizing derivative information to provide a fast algortihm to find the inducing points $a,b$. I would also appreciate help in cases were $x^{*} \in \mathbb{R}^{d}$. Some good references on this topic would be of great help.
What are the best and most efficient techniques that can be utilizaed for the gaussain process. Specifically, I am looking for possibly utilizing derivative information to provide a fast algortihm to find the inducing points $a,b$. I would also appreciate help in cases were $x^{*} \in \mathbb{R}^{d}$. Some good references on this topic would be of great help.
PS: The intent here is to estimate the input points which would cause a decrease or increase in the response