5

I'm reading Introduction to Statistical Learning. The relevant part is referenced here: Proof/Derivation of Residual Sum of Squares (Based on Introduction to Statistical Learning).

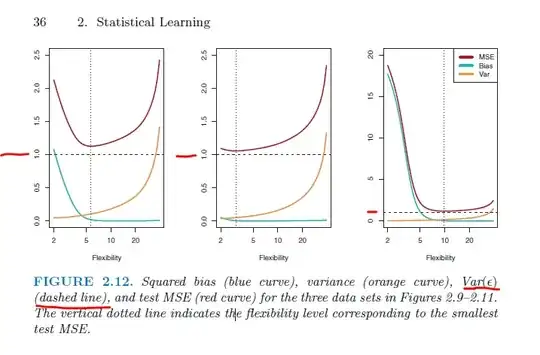
When the author shows graphs that illustrate "Bias vs Variance Tradeoff" (as in Figure 2.12), the ${\rm Var}(\varepsilon)$ is always $1$ (note the dashed lines in the figures):

three graphs of MSE on y-axis; flexibility on x-axis, and Var(epsilon) is always at 1

The conditions of $\varepsilon$ are clarified elsewhere, as on page 16:

$\varepsilon$ is a random error term, which is independent of $X$ and has mean zero.

... and there is some explanation about going from "random error term" to "irreducible error":

However, even if it were possible to form a perfect estimate for $f$, so that our estimated response took the form $\hat{Y} = f(X)$, our prediction would still have some error in it! This is because $Y$ is also a function of $\varepsilon$, which, by definition, cannot be predicted using $X$. Therefore, variability associated with $\varepsilon$ also affects the accuracy of our predictions.

But I don't see anywhere in the other SO questions, nor in the book: why is $Var(\varepsilon)$ always at 1?

  • Is it because the "mean is zero"? I don't think so; I could describe a dataset with mean of zero but a variance of $\ne 1$.
  • Is it because, as described elsewhere, the "the error term $\varepsilon$ is normally distributed"? I don't know enough about the normal distribution; is the variance of a normal distribution is always equal to some value?

EDIT

In looking for help in Wikipedia's MSE article, I expected to find a consistent formula with the "three fundamental quantities" (i.e., the variance, the bias, and the variance of the error terms), but I didn't. Can someone tell me why the Wikipedia doesn't list the variance of error terms:

$$\operatorname{MSE}(\hat{\theta})=\operatorname{Var}(\hat{\theta})+ \left(\operatorname{Bias}(\hat{\theta},\theta)\right)^2$$

The Red Pea
  • 306
  • 2
  • 15
  • 2
    When doing examples, people will often just set the variance of the error term $\epsilon$ equal to 1. If they didn't want to fix a value for $Var(\epsilon) = \sigma^2$ then they wouldn't have been able to make those plots with particular numbers on the side. – jld Aug 09 '16 at 01:23
  • So is it just convention? Why 1? 1 is convenient? No other assumptions about error term can lead us to this effect? ( I realize I am probably over thinking something that is, by definition, unknowable...) – The Red Pea Aug 09 '16 at 01:25
  • Author does say, "...the irreducible error will always provide an upper bound on the accuracy of our prediction for $Y$. This bound is almost always unknown in practice" Is this as good as admitting that 1 is an arbitrary choice? – The Red Pea Aug 09 '16 at 01:27
  • 3
    also this has absolutely no bearing on real data. This is purely for the sake of the examples that they're doing. In real life $Var(\epsilon)$ could be anything – jld Aug 09 '16 at 01:29
  • Thanks @Chaconne, you should've answered so I could upvote a tortoise. Can we calculate $Var(\epsilon)$ in real life? Or is that the "unknown" author describes in practice – The Red Pea Aug 09 '16 at 02:25
  • Also I thought you left a comment showing (another reason) how 1 was mathematically convenient... Did you? Just interesting how frequently I am encountering " mathematical convenience " is part of a rationale in statistics, as in the question, "why square the difference of means?" – The Red Pea Aug 09 '16 at 02:35

1 Answers1

3

It isn't because the mean is $0$ or because the error term is normally distributed. In fact, the normal distribution is the only 'named' distribution where the mean and the variance are independent of each other (see: What is the most surprising characterization of the Gaussian (normal) distribution?).

More generally, my strong guess is that the purpose of setting the variance of the errors equal to $1$ is pedagogical. Everything in the figures can be related to the variance of the error term because the unit of measurement in the figures is $1$ and that was set as the variance of the error term.

Regarding the Wikipedia article, be aware that the variance of theta is a function of the variance of the error term, so ${\rm Var}(\hat\theta)$ does include ${\rm Var}(\varepsilon)$ (it's just out of sight).

Community
  • 1
gung - Reinstate Monica
  • 132,789
  • 81
  • 357
  • 650
  • Thank you. This characterization of normal distributions - you're saying I could have both conditions: normal distribution and mean of 0, and still know absolutely nothing about variance? Relatedly, is it true that a mean of zero is a characteristic/definition of error terms while the variance of error terms could be whatever I want and they're still error terms? – The Red Pea Aug 09 '16 at 02:42
  • 1
    @TheRedPea, yes. For a regression model, the mean of the errors is 0 by definition. But the variance can be any positive value. – gung - Reinstate Monica Aug 09 '16 at 03:53
  • The importance of the concept of "mean of errors approaching zero"... I did not realize it was so fundamental as [described on NIST](http://www.itl.nist.gov/div898/handbook/pmd/section2/pmd212.htm) , but the way the describe it... Please confirm: It does not mean there **is no** "drift" , that would be wrong interpretation,, but that regression models do not attempt to account for such drift? ( as the regression which attempted to do that in, the case of drift, would have a very nonzero error?) Thanks again, gung, these dialogues are helpful for me... – The Red Pea Aug 09 '16 at 06:47
  • 1
    @TheRedPea, that's really a different question (& I'm not sure I follow your question). You should ask this as a new question to get a better answer & so the information won't be buried in comments. – gung - Reinstate Monica Aug 09 '16 at 11:44