15

When initializing connection weights in a feedforward neural network, it is important to initialize them randomly to avoid any symmetries that the learning algorithm would not be able to break.

The recommendation I have seen in various places (eg. in TensorFlow's MNIST tutorial) is to use the truncated normal distribution using a standard deviation of $\dfrac{1}{\sqrt{N}}$, where $N$ is the number of inputs to the given neuron layer.

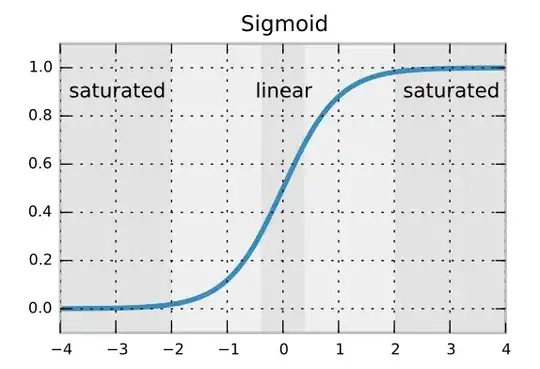
I believe that the standard deviation formula ensures that backpropagated gradients don't dissolve or amplify too quickly. But I don't know why we are using a truncated normal distribution as opposed to a regular normal distribution. Is it to avoid rare outlier weights?

MiniQuark
  • 1,930
  • 3
  • 16
  • 29
  • 1
    Can you provide source of this recommendation and/or the direct quotation? – Tim Aug 07 '16 at 17:54
  • +Tim Good point, I added a link to an example. I believe I also saw this recommendation in a paper about neural network good practices (can't find it, though). – MiniQuark Aug 07 '16 at 18:18

2 Answers2

14

I think its about saturation of the neurons. Think about you have an activation function like sigmoid.

enter image description here

If your weight val gets value >= 2 or <=-2 your neuron will not learn. So, if you truncate your normal distribution you will not have this issue(at least from the initialization) based on your variance. I think thats why, its better to use truncated normal in general.

Güngör Basa
  • 256
  • 2
  • 5
6

The truncated normal distribution is better for the parameters to be close to 0, and it's better to keep the parameters close to 0. See this question: https://stackoverflow.com/q/34569903/3552975

enter image description here

Three reasons to keep the parameters small(Source: Probabilistic Deep Learning: with Python, Keras and Tensorflow Probability):

  1. Experience shows that trained NNs often have small weights.
  2. Smaller weights lead to less extreme outputs (in classification, less extreme probabilities), which is desirable for an untrained model.
  3. It’s a known property of prediction models that adding a component to the loss function, which prefers small weights, often helps to get a higher prediction performance. This approach is also known as regularization or weight decay in non-Bayesian NNs.

And in this blog: A Gentle Introduction to Weight Constraints in Deep Learning, Dr. Jason Brownlee states that:

Smaller weights in a neural network can result in a model that is more stable and less likely to overfit the training dataset, in turn having better performance when making a prediction on new data.

If you employ ReLU you'd better make it with a slightly positive initial bias:

One should generally initialize weights with a small amount of noise for symmetry breaking, and to prevent 0 gradients. Since we're using ReLU neurons, it is also good practice to initialize them with a slightly positive initial bias to avoid "dead neurons".

Lerner Zhang
  • 5,017
  • 1
  • 31
  • 52
  • I'm not sure how using the truncated_normal will prevent dead neurons: it won't add any "slightly positive initial bias". Can you please elaborate? – MiniQuark Mar 01 '17 at 15:06
  • 2
    because the backpropagation will only update 'live' neurons, with some nonzero contribution to the propagation – Jason Jul 29 '18 at 10:55
  • @MiniQuark You are right. I have updated my answer. – Lerner Zhang Sep 16 '21 at 14:03
  • 1
    Can you edit your first paragraph? It seems to be missing a few words. // The quotation from the SNN paper is specifically about the self-normalizing network. It's not a general claim that all 0-mean, unit-variance activations will be propagated through the network, which they demonstrate by comparing SNNs to standard FFNs. – Sycorax Sep 16 '21 at 14:09
  • @Sycorax Is it better now? Any further suggestions would be appreciated. – Lerner Zhang Sep 16 '21 at 14:15