Name for "probability density elasticity" property?

Question

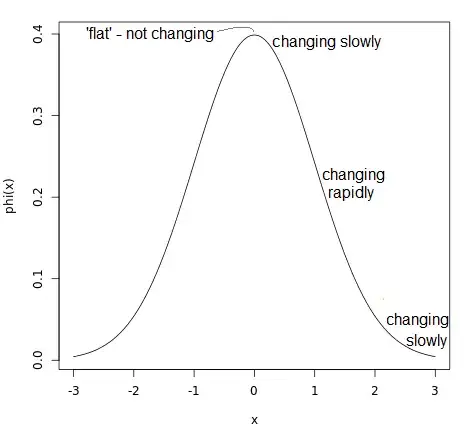
For standard normal Z, the change in probability density associated with equally sized changes in z is obviously greater for values of z that are further away from the mean/mode.

For example, if z=0, then $\phi(z)- \phi(z+0.1)\approx 0.002$. However, if z=2, then $\phi(z)-\phi(z+0.1) \approx 0.01$. Thus the density change associated with increasing z by 0.01 is 5 times as large in the latter case.

I have two questions related to this.

1. Does this property (or a similar property) have a name? (That is, the property where for rv X with PDF f and mean value $\bar{x}$: $\frac{\partial f(x)}{\partial x}<\frac{\partial f(x^o)}{x^o}$ when $\lvert x^o- \bar{x} \rvert >\lvert x- \bar{x} \rvert$.) Does this general idea - that is the extent to which the PDF's derivative changes over the distribution's support - have a name?

2. Are probability distributions with this property (or a similar property) systematically classified? Can they be identified in some straightforward way? Obviously, all normal distributions have it, but do all unimodal continuous finite distributions?

I am asking because I am working with a finding that is dependent on the above property and I'd like to figure out the best way to succinctly talk about it, and also how to accurately think and report about its generality (or lack thereof).

Answer 1

Note (proceeding somewhat loosely and assuming the necessary derivatives exist and so on for it all to work) that $f(x+\delta)\approx f(x) + \delta f'(x)$ (e.g. consider a first order Taylor expansion) and so the rate of change $\frac{f(x+\delta)-f(x)}{x+\delta-x}\approx f'(x)$. Indeed in the limit as $\delta$ becomes small this will become the result.

So you're effectively saying "why is $|\phi'(x)|$ at $x=0$ smaller than elsewhere?".

The answer is that the function $\phi(x)$ is flat when you're at the top of the hill (any mode of a continuously differentiable density):

The normal has only one mode. The derivative is $0$ there, and non-zero everywhere else. Let's look at a plot of $|\phi'(x)|$:

Clearly it's bigger everywhere than at the mode (= mean = 0).

This function (the absolute value of the derivative of the density) doesn't have any particular name I am aware of.

The absolute derivative of any other normal will follow the same pattern about its mode.

Obviously, all normal distributions have it, but do all unimodal continuous finite distributions?

No. First we have to get away from saying mean/mode. In general the mean and mode aren't in the same place. The mean may well be situated in a place where the derivative is large. So lets focus on the mode.

• It's perfectly possible to have a unimodal density where the derivative is 0 not at a mode.