How to sample value from Symmetric Geometric Distribution

Question

How can I sample a value from a symmetric geometric distribution, as defined in this link.

There, the density of the symmetric geometric proposal distribution is given by \begin{equation*} f(\theta;p_g)\propto \frac{p_g (1 - p_g)^{|\theta|}}{2(1- p_g)}, \end{equation*} where the symmetry centers at $\theta$. However, it seems that this distribution is not widely known under this name. It seems that this distribution is somehow related to the Laplace distribution, for which I know how to sample values, but I couldn't establish this relation myself.

As such, my question is actually twofold:

1. Is this distribution known under a more common name, and
2. Is there any other distribution I can relate it to, in order to generate values from this distribution more easily?

Answer 1

The linked document is unclear; it doesn't even indicate the random variable (which I will call $X$). I assume it means $p_g$ & $\theta$ are parameters. It doesn't define the values taken by $X$ - which I believe should appear in the exponent as $|x-\theta|$ not as $|\theta|$ - nor the values taken by $\theta$ (which I presume to be integer) and it refers to the distribution as discrete but calls it a density.

I believe a correct implementation of a "symmetric geometric" is as follows:

$$p_X(x;\theta,p_g)= \frac{p_g (1 - p_g)^{\mid x-\theta\mid}}{2- p_g},\: x\in \mathbb{Z};\, \theta\in \mathbb{Z}, 0<p_g<1$$

(note the change in the denominator also)

This distribution has the property that as you move out from the center, the ratio of probability to the next probability further into the tail remains constant (in geometric ratio). This is what makes it "geometric".

Here's an example, with $p_g=0.3$ and $\theta=10$:

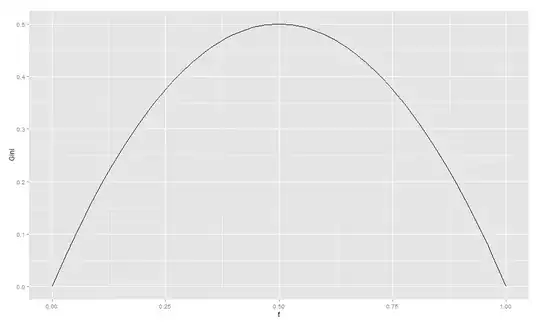
As you see it's symmetric, geometric and centered at $\theta$.

If the distribution has (sub)exponential tails, that should work fine as a proposal.

What they attempted to define (but failed to) is slightly different:

$$p_X(x;\theta,p_g)= \frac{p_g (1 - p_g)^{|x-\theta|}}{2(1- p_g)},\: x\in \mathbb{Z};\, \theta\in \mathbb{Z}, 0<p_g<1$$

This is not in geometric ratio, because the central spike is twice the height it should be to be in the same ratio to the values either side as those values are to the ones further out again.

While I don't think it merits the names symmetric geometric, this distribution can be generated by generating a geometric (the version indexed from 0), attaching a random sign and shifting by $\theta$ (i.e. add $\theta$).

(The one I defined in the beginning is slightly more complicated to generate, but one way to do it is as above but if you generate a $-0$ you throw it out and generate again.)

---

A different one suitable for heavier tails would be a discrete equivalent of a table-mountain distribution, such as

$$p_X(x;\theta,p_g)= \frac{\min(1,\mid\! x-\theta\!\mid^{-s})}{2\zeta(s)+1},\: x\in \mathbb{Z};\, \theta\in \mathbb{Z},s>1$$

(specifically with $s=2$ for the usual table mountain proposal).

This is effectively a symmetric version of a zeta(s) distribution with a "flat" bit at $\theta$ (in that it has the same probability as the values either side of it). You could replace the value in the numerator at $\theta$ (i.e. $1$) with an arbitrary positive value (if you also fix the denominator), or expand the "flat" part (ditto) or use a different $s$ if needed.

Answer 2

I mostly agree with @Glen_b but I think the correct probability function is

$$f(\theta) = \begin{cases} p_g &\theta = 0\\ \frac{1}{2}p_g(1-p_g)^{|\theta|-1} &\theta \neq 0\end{cases}$$

for integer $\theta$. This seems to be the only way to get the correct variance, and it is the same as the given formula up to a scalar. As Glen_b said, a draw from this distirbution can be obtained by drawing from a geometric distirbution and multiplying the result by a uniform random choice of $+1$ or $-1$. You can work this out by hand and/or verify it by simulation.

I also agree that the intention is probably that the proposed value $\theta_{new}$ is meant to be $\theta + x$ where $x$ is a random draw from $f$. This is the only way I can see for the text in your link to make sense.

Unfortunately, we cannot know for sure because we don't have access to the source!

Answer 3

Discrete Laplace distribution is a very similar to the one you describe (check Inusah and Kozubowski, 2006, and Kotz, Kozubowski and Podgorski, 2012).

Discrete Laplace distribution has probability mass function:

$$ f(x) = \frac{1-p}{1+p} p^{|x-\mu|} $$

and cumulative distribution function

$$ F(x) = \left\{\begin{array}{ll} \frac{p^{-|x-\mu|}}{1+p} & x < 0 \\ 1 - \frac{p^{|x-\mu|+1}}{1+p} & x \ge 0 \end{array}\right. $$

The name discrete Laplace comes from the fact that if $U \sim \mathrm{Geometric}(1-p)$ and $V \sim \mathrm{Geometric}(1-p)$, then $U-V \sim \mathrm{DiscreteLaplace}(p)$, where geometric distribution is related to discrete Laplace distribution in similar way as exponential distribution is related to Laplace distribution.

Sampling from it is straightforward: you draw $U$ and $V$ from geometric distribution parametrized by $q = 1-p$, and then take $U-V$.

In R it is implemented in DiscreteLaplace, disclap and extraDistr packages.

Below you can see your distribution (in black) and discrete Laplace distribution (in red) parametrized by different values of $p$ (for discrete Laplace by $1-p$). As you can see, they differ but the idea behind them is very similar.

---

Kotz, S., Kozubowski, T., & Podgorski, K. (2012). The Laplace distribution and generalizations: a revisit with applications to communications, economics, engineering, and finance. Springer Science & Business Media.

Inusah, S., & Kozubowski, T.J. (2006). A discrete analogue of the Laplace distribution. Journal of statistical planning and inference, 136(3), 1090-1102.