39

This is probably an amateur question, but I am interested in how did the scientists come up with the shape of the normal distribution probability density function? Basically what bugs me is that for someone it would perhaps be more intuitive that the probability function of normally distributed data has a shape of an isosceles triangle rather than a bell curve, and how would you prove to such a person that the probability density function of all normally distributed data has a bell shape? By experiment? Or by some mathematical derivation?

After all what do we actually consider normally distributed data? Data that follows the probability pattern of a normal distribution, or something else?

Basically my question is why does the normal distribution probability density function has a bell shape and not any other? And how did scientists figure out on which real life scenarios can the normal distribution be applied, by experiment or by studying the nature of various data itself?

So I've found this link to be really helpful in explaining the derivation of the functional form of the normal distribution curve, and thus answering the question "Why does the normal distribution look like it does and not anything else?". Truly mindblowing reasoning, at least for me.

whuber
  • 281,159
  • 54
  • 637
  • 1,101
bonehead
  • 536
  • 1
  • 4
  • 11
  • 3
    Check out [this question](http://stats.stackexchange.com/q/129417/22228) - it isn't true to claim that only the normal distribution is "bell-shaped". – Silverfish Aug 03 '16 at 10:49
  • So basically what I've concluded from reading the question you linked is that no specific distribution is preferred over any other, and the name "normal" doesn't really implicate anything except that the data follows a particular distribution. If you have a data set, there isn't any distribution that promises a good fit for your set, or a distribution that is somewhat superior to others, you simply try to find the best fit for your data set. So basically a triangular distribution is just as "normal" as the normal distribution (normal in the broad sense of the word) ? – bonehead Aug 03 '16 at 11:01
  • 11
    The normal distribution has some vitally important statistical properties, that make it a special object of study and also mean it often arises "naturally", eg as the limiting case of other distributions. See in particular the [Central Limit Theorem](https://en.wikipedia.org/wiki/Central_limit_theorem). However, it just isn't the only distribution that peaks in the middle and has tails either side. People often assume such data is normal because the histogram "looks bell-shaped", but my linked answer shows how there are many other candidate distributions for such data sets. – Silverfish Aug 03 '16 at 11:14
  • 5
    Note that statisticians didn't discover the normal distribution by looking at many datasets and realising this density function was empirically a good fit for many of them. As you wonder in your question, there was a process of mathematical investigation of certain problems in probability theory, to which the normal distribution "pops out" as an answer. This is well-explained in e.g. [this answer here](http://stats.stackexchange.com/a/111332/22228). – Silverfish Aug 03 '16 at 11:15
  • 1
    So what I've understood so far is that by studying certain real life probability problems the binomial distribution was discovered and found to be applicable in many situations. However, by increasing the number of trials (x becomes continuous) they found that the binomial distribution approaches a curve shape that we now know as the normal distribution. Then an expression for the probability density function of the normal distribution was found, and from there various scientists discovered independently that the normal distribution can be applied to many real life situations. – bonehead Aug 03 '16 at 11:56
  • 3
    And basically if someone asked me to explain to them why is the normal distribution "normal", I would need to explain them the history of the normal distribution which is lengthy and complex in itself starting from the binomial distribution and so forth, and then perhaps prove the central limit theorem, and show that the normal distribution is applicable in studying many situations in real life. – bonehead Aug 03 '16 at 11:59
  • @ahra When somebody asks you why a normal distribution is "normal", there are many possible correct answers to that question. An historical explanation doesn't immediately come to mind. I usually tell people that a normal distribution arises in observing values with many unobserved sources of error. – AdamO Aug 03 '16 at 13:03
  • 5
    You can visualize the shape of a normal distribution using [one of these nifty devices](https://www.youtube.com/watch?v=xDIyAOBa_yU) called Galton boards. Actually that's a binomial distribution, but, you know, central limit theorem. – Federico Poloni Aug 03 '16 at 13:23
  • 1
    ahra -- I don't find the reasoning at the link particularly convincing. In particular, the setup of the problem is not adequately justified (why those particular criteria and not something else - similar criteria, but not the same), which makes the resulting differential equation look like it has been set up to give the desired result. It's more *if* we choose these properties, we get the normal. That's all well and good but it doesn't make the normal any more obvious or natural than some obvious alternatives (such as some of those considered by Laplace). ... ctd – Glen_b Aug 04 '16 at 01:19
  • ctd ... The later part on the approximation of the binomial is pretty standard, but much of the background for what's there we can largely attribute to de Moivre – Glen_b Aug 04 '16 at 01:21
  • @FedericoPoloni Also called a [quincunx](https://en.wikipedia.org/wiki/Quincunx). :) – Alexis Dec 14 '21 at 06:20

6 Answers6

44

You seem to assume in your question that the concept of the normal distribution was around before the distribution was identified, and people tried to figure out what it was. It's not clear to me how that would work. [Edit: there is at least one sense it which we might consider there being a "search for a distribution" but it's not "a search for a distribution that describes lots and lots of phenomena"]

This is not the case; the distribution was known about before it was called the normal distribution.

how would you prove to such a person that the probability density function of all normally distributed data has a bell shape

The normal distribution function is the thing that has what is usually called a "bell shape" -- all normal distributions have the same "shape" (in the sense that they only differ in scale and location).

Data can look more or less "bell-shaped" in distribution but that doesn't make it normal. Lots of non-normal distributions look similarly "bell-shaped".

The actual population distributions that data are drawn from are likely never actually normal, though it's sometimes quite a reasonable approximation.

This is typically true of almost all the distributions we apply to things in the real world -- they're models, not facts about the world. [As an example, if we make certain assumptions (those for a Poisson process), we can derive the Poisson distribution -- a widely used distribution. But are those assumptions ever exactly satisfied? Generally the best we can say (in the right situations) is that they're very nearly true.]

what do we actually consider normally distributed data? Data that follows the probability pattern of a normal distribution, or something else?

Yes, to actually be normally distributed, the population the sample was drawn from would have to have a distribution that has the exact functional form of a normal distribution. As a result, any finite population cannot be normal. Variables that necessarily bounded cannot be normal (for example, times taken for particular tasks, lengths of particular things cannot be negative, so they cannot actually be normally distributed).

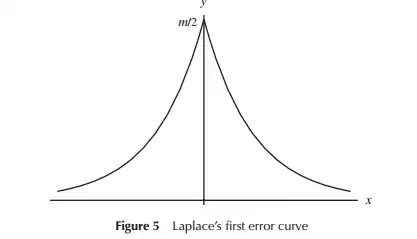
it would perhaps be more intuitive that the probability function of normally distributed data has a shape of an isosceles triangle

I don't see why this is necessarily more intuitive. It's certainly simpler.

When first developing models for error distributions (specifically for astronomy in the early period), mathematicians considered a variety of shapes in relation to error distributions (including at one early point a triangular distribution), but in much of this work it was mathematics (rather than intuition) that was used. Laplace looked at double exponential and normal distributions (among several others), for example. Similarly Gauss used mathematics to derive it at around the same time, but in relation to a different set of considerations than Laplace did.

In the narrow sense that Laplace and Gauss were considering "distributions of errors", we could regard there as being a "search for a distribution", at least for a time. Both postulated some properties for a distribution of errors they considered important (Laplace considered a sequence of somewhat different criteria over time) led to different distributions.

Basically my question is why does the normal distribution probability density function has a bell shape and not any other?

The functional form of the thing that is called the normal density function gives it that shape. Consider the standard normal (for simplicity; every other normal has the same shape, differing only in scale and location):

$$f_Z(z) = k \cdot e^{-\frac12 z^2};\;-\infty<z<\infty$$

(where $k$ is simply a constant chosen to make the total area 1)

this defines the value of the density at every value of $x$, so it completely describes the shape of the density. That mathematical object is the thing we attach the label "normal distribution" to. There's nothing special about the name; it's just a label we attach to the distribution. It's had many names (and is still called different things by different people).

While some people have regarded the normal distribution as somehow "usual" it's really only in particular sets of situations that you even tend to see it as an approximation.

The discovery of the distribution is usually credited to de Moivre (as an approximation to the binomial). He in effect derived the functional form when trying to approximate binomial coefficients (/binomial probabilities) to approximate otherwise tedious calculations but - while he does effectively derive the form of the normal distribution - he doesn't seem to have thought about his approximation as a probability distribution, though some authors do suggest that he did. A certain amount of interpretation is required so there's scope for differences in that interpretation.

Gauss and Laplace did work on it in the early 1800s; Gauss wrote about it in 1809 (in connection with it being the distribution for which the mean is the MLE of the center) and Laplace in 1810, as an approximation to the distribution of sums of symmetric random variables. A decade later Laplace gives an early form of central limit theorem, for discrete and for continuous variables.

Early names for the distribution include the law of error, the law of frequency of errors, and it was also named after both Laplace and Gauss, sometimes jointly.

The term "normal" was used to describe the distribution independently by three different authors in the 1870s (Peirce, Lexis and Galton), the first in 1873 and the other two in 1877. This is more than sixty years after the work by Gauss and Laplace and more than twice that since de Moivre's approximation. Galton's use of it was probably most influential but he used the term "normal" in relation to it only once in that 1877 work (mostly calling it "the law of deviation").

However, in the 1880s Galton used the adjective "normal" in relation to the distribution numerous times (e.g. as the "normal curve" in 1889), and he in turn had a lot of influence on later statisticians in the UK (especially Karl Pearson). He didn't say why he used the term "normal" in this way, but presumably meant it in the sense of "typical" or "usual".

The first explicit use of the phrase "normal distribution" appears to be by Karl Pearson; he certainly uses it in 1894, though he claims to have used it long before (a claim I would view with some caution).

References:

Miller, Jeff
"Earliest Known Uses of Some of the Words of Mathematics:"
Normal distribution (Entry by John Aldrich)
http://jeff560.tripod.com/n.html
(alternate: https://mathshistory.st-andrews.ac.uk/Miller/mathword/n/)

Stahl, Saul (2006),
"The Evolution of the Normal Distribution",
Mathematics Magazine, Vol. 79, No. 2 (April), pp 96-113
https://www.maa.org/sites/default/files/pdf/upload_library/22/Allendoerfer/stahl96.pdf

Normal distribution, (2016, August 1).
In Wikipedia, The Free Encyclopedia.
Retrieved 12:02, August 3, 2016, from
https://en.wikipedia.org/w/index.php?title=Normal_distribution&oldid=732559095#History

Hald, A (2007),
"De Moivre’s Normal Approximation to the Binomial, 1733, and Its Generalization",
In: A History of Parametric Statistical Inference from Bernoulli to Fisher, 1713–1935; pp 17-24

[You may note substantial discrepancies between these sources in relation to their account of de Moivre]

Glen_b
  • 257,508
  • 32
  • 553
  • 939
  • Thank you for the in-depth answer! I've looked further into how the shape of the normal distribution was derived and I've found this document http://courses.ncssm.edu/math/Talks/PDFS/normal.pdf, and I have a problem understanding how can we assume that the errors do not depend on the orientation of the coordinate system (an assumption that enables an important conclusion later on), when it seems to me that such an assumption would only hold in the example of darts, but not in the example of accidental experimental errors. – bonehead Aug 03 '16 at 13:22
  • Actually the whole darts approach confuses me since I'm studying normal distribution in the context of accidental experimental errors. I'm guessing that the darts approach assumes that you can make independent errors in two dimensions which is okay in the context used but is unclear to me to what would it translate in the context of experimental errors where you have a dependant and an independant variable which means you can make an error only in one dimension. – bonehead Aug 03 '16 at 13:39
  • 1
    Great use of references. +1 – Aaron Hall Aug 03 '16 at 20:17
  • 2
    I think "central limit theorem" should be mentioned here somewhere, since the OP seems (at least in part) to be asking why this particular distribution is so prevalent. – joc Aug 04 '16 at 09:39
  • 1
    @joc I don't see the question asking about prevalence or even suggesting a question about it. However, I do talk about de Moivre's work relating to the binomial and about Laplace's work relating to normal approximations for sums of symmetric random variables ... which are more directly related to the question. However, I'll add a sentence relating to Laplace's work on the problem (though it wouldn't be be called that for another century). – Glen_b Aug 04 '16 at 10:18
  • Great answer -- I might be being silly, but shouldn't $f_z(z)$ be $f_z(x)$? – Landak Aug 04 '16 at 13:36
  • @Landak Not silly at all; I'll make the variable consistent. – Glen_b Aug 04 '16 at 16:22
26

"The Evolution of the Normal Distribution" by SAUL STAHL is the best source of information to answer pretty much all the questions in your post. I'll recite a few points for your convenience only, because you'll find the detailed discussion inside the paper.

This is probably an amateur question

No, it's an interesting question to anyone who uses statistics, because this is not covered in detail anywhere in standard courses.

Basically what bugs me is that for someone it would perhaps be more intuitive that the probability function of normally distributed data has a shape of an isosceles triangle rather than a bell curve, and how would you prove to such a person that the probability density function of all normally distributed data has a bell shape?

Look at this picture from the paper. It shows the error curves that Simpson came up with before Gaussian (Normal) was discovered to analyze experimental data. So, your intuition is spot on.

enter image description here

By experiment?

Yes, that's why they were called "error curves". The experiment was astronomical measurements. Astronomers struggled with measurement errors for centuries.

Or by some mathematical derivation?

Again, YES! Long story short: the analysis of errors in astronomical data led Gauss to his (aka Normal) distribution. These are the assumptions he used:

enter image description here

By the way, Laplace used a few different approaches, and also came up with his distribution too while working with astronomical data:

enter image description here

As to why normal distribution shows in experiment as measurement errors, here's a typical "hand-wavy" explanation physicist are used to give (a quote from Gerhard Bohm, Günter Zech, Introduction to Statistics and Data Analysis for Physicists p.85):

Many experimental signals follow to a very good approximation a normal distribution. This is due to the fact that they consist of the sum of many contributions and a consequence of the central limit theorem.

Aksakal
  • 55,939
  • 5
  • 90
  • 176
  • 2
    The Stahl reference addresses the original question very much from the angle that it was posed from - that's a really nice find. – Silverfish Aug 04 '16 at 17:10
  • The Stahl paper confirmed for me that the binomial distribution (and thus Pascal's triangle) is the genesis for the bell curve shape and mathematical construction. Nice to see this, finally. – JTP - Apologise to Monica Feb 08 '20 at 19:31
  • The link for the paper by Saul Stahl isn't working anymore. However, the same paper can be downloaded from https://www.researchgate.net/publication/255668423_The_Evolution_of_the_Normal_Distribution – Dr Nisha Arora Jun 13 '20 at 17:20
  • @DrNishaArora the link is still working for me, interesting – Aksakal Jun 13 '20 at 17:22
  • @Aksakal Even when I googled, the first link it was showing was the same as mentioned by you and page was unable to load, so I downloaded the paper from the research-gate. – Dr Nisha Arora Jun 13 '20 at 17:51
11

The "normal" distribution is defined to be that particular distribution.

The question is why would we expect this particular distribution to be common in nature, and why is it so often used as an approximation even when the real data does not exactly follow that distribution? (Real data is often found to have a "fat tail", i.e. values far from the mean are much more common than the normal distribution would predict).

To put it another way, what is special about the normal distribution?

The normal has a lot of "nice" statistical properties, (see e.g. https://en.wikipedia.org/wiki/Central_limit_theorem), but the most relevant IMO is the fact that is the "maximum entropy" function for any distribution with a given mean and variance. https://en.wikipedia.org/wiki/Maximum_entropy_probability_distribution

To express this in ordinary language, if you are given only the mean (central point) and variance (width) of a distribution, and you assume nothing else whatsoever about it, you will be forced to draw a normal distribution. Anything else requires additional information (in the sense of Shannon information theory), for example skewness, to determine it.

The principle of maximum entropy was introduced by E.T. Jaynes as a way of determining reasonable priors in Bayesian inference, and I think he was the first to draw attention to this property.

See this for further discussion: http://www.inf.fu-berlin.de/inst/ag-ki/rojas_home/documents/tutorials/Gaussian-distribution.pdf

gareth
  • 141
  • 4
  • 6
    "In other words if you are given only the mean (central point) and variance (width) of a distribution, and you assume nothing else whatsoever about it, you will be forced to draw a normal distribution." I guess that depends on what the definition of "forced" is. You may be forced. I would not be. What you have described is the moral equivalent of being "forced" to assume a function is linear when you don't know its form, or that random variables are independent when you don't know their exact dependence. I have not, am not, and will not be forced to make any of these assumptions. – Mark L. Stone Aug 03 '16 at 17:39
  • @MarkL.Stone You are forced to by the *principle of maximum entropy*. You should read Jaynes for an overview. All exponential families are justified by this principle. – Neil G Aug 03 '16 at 17:52
  • 5
    @Neil I believe part of Mark's point may be that *justification* is not *compulsion.* – whuber Aug 03 '16 at 18:40
  • @whuber: The compulsion is clearly stated in the answer *"and you assume nothing else whatsoever about it"*. With that stipulation, you are absolutely compelled. – Neil G Aug 03 '16 at 18:43
  • 5
    @Neil Far from it! First you have to assume the principle of maximum entropy is useful and applicable to your statistical problem. Next you have to be absolutely certain there's nothing else you can assume about the distribution. Both of those are problematic. (In most statistical problems I have encountered--outside the realm of theoretical physics--the former has not been true; and I have never seen a real-world problem where the latter is the case.) – whuber Aug 03 '16 at 18:46
  • @whuber: Well, about "being absolutely certain there's nothing else you can assume about the distribution" is specifically stated as a condition "*if* you assume nothing else whatsoever…" So, we are assuming that — and if you can't assume that, then we're not talking about this answer. As for assuming the principle of maximum entropy, well, we have a fundamental disagreement about what it means to choose a minimally assumptive distribution. – Neil G Aug 03 '16 at 18:49
  • I think the "force to draw" bit should be reworded according to these comments. It appears that, if you explore the deepest darkest corners of its meaning, there's a disagreement about what it might mean. For those with a lesser background, it is very misleading (I regularly use uniform distributions instead when they are more convenient, so "forced" doesn't feel quite right). Given that it's debated at the highest levels, and worse at lower levels, changing the wording may help clarify, even if it turned out that "forced" was indeed the correct word. – Cort Ammon Aug 04 '16 at 01:06
  • 1
    @Neil Mark and whuber. I have tried to clarify that paragraph. I think "assume nothing else whatsoever" is a reasonable ordinary language explanation of what the principle of maximum entropy is trying to do. Being ordinary language you could of course put a different interpretation on it. That is why we need the maths. The more precise statement is that we are adding no information, in the sense of Shannon. The links explain this further. – gareth Aug 04 '16 at 14:01
  • @Neil PS the uniform distribution is the maximum entropy distribution given no constraints. – gareth Aug 04 '16 at 14:10
  • 1
    @gareth a uniform distribution on all the reals (which I think you meant in your latest comment) would be a highly improper distribution. Your claim of maximum entropy as your driver towards a normal distribution makes a major assumption; why it is any more forceful than assuming something else, such as minimum range? – Henry Aug 04 '16 at 14:42
  • 1
    @Henry A uniform distribution on the reals is an improper distribution, but improper priors can be useful, if the posterior distribution ends up well-behaved. If you restrict the distribution to a finite range then the top-hat function is the maxent distribution. The question is, when would that be a realistic assumption? The normal is not the only maxent function - it is just the maxent function *when given the mean and variance as constraints*. If you take the mean error (instead of the mean squared error) as given, then you get the Laplace function as the maxent distribution. – gareth Aug 05 '16 at 12:42
  • 1
    @Henry As for why use maxent rather than some other principle, as I said, it corresponds to not adding in any constraints other than those you have stated explicitly. This is provable in terms of Shannon information. But if you have a better definition of information, by all means use it. If you have any real world knowledge of the distribution other than its mean and variance you should make use of that too. See the linked Wikipedia article for a table of maxent functions and corresponding constraints. – gareth Aug 05 '16 at 12:48
3

The Normal Distribution (aka "Gaussian Distribution") has a firm mathematical foundation. The Central Limit Theorem says that if you have a finite set of n independent and identically distributed random variables having a specific mean and variance, and you take the average of those random variables, the distribution of the result will converge to a Gaussian Distribution as n goes to infinity. There is no guesswork here, since the mathematical derivation leads to this specific distribution function and no other.

To put this into more tangible terms, consider a single random variable, such as flipping a fair coin (2 equally possible outcomes). The odds of getting a particular outcome is 1/2 for heads and 1/2 for tails.

If you increase the number of coins and keep track of the total number of heads obtained with each trial, then you will get a Binomial Distribution, which has a roughly bell shape. Just graph with the number of heads along the x-axis, and the number of times you flipped that many heads along the y-axis.

The more coins you use, and the more times you flip the coins, the closer the graph will come to looking like a Gaussian bell curve. That's what the Central Limit Theorem asserts.

The amazing thing is that the theorem does not depend on how the random variables are actually distributed, just so long as each of the random variables has the same distribution. One key idea in the theorem is that you are adding or averaging the random variables. Another key concept is that the theorem is describing the mathematical limit as the number of random variables becomes larger and larger. The more variables you use, the closer the distribution will approach a Normal Distribution.

I recommend you take a class in Mathematical Statistics if you want to see how mathematicians determined that the Normal Distribution is actually the mathematically correct function for the bell curve.

user126665
  • 31
  • 1
  • Thank you for your contribution. It would be correct if you were to explain that the distribution of the sum (or mean) *must be standardized.* Otherwise, the distribution of the sum does not approach a limit and the distribution of the mean approaches a constant. But how does this post answer the questions that were posed? (Admittedly, there are various questions being posed and they are all confused and vague, but they seem to be asking about how the formula for the Gaussian PDF was discovered or derived.) – whuber Aug 04 '16 at 22:16
2

There are some excellent answers on this thread. I can't help feeling the OP wasn't asking the same question as everyone wants to answer. I get that, though, because this is close to being one of the most exciting questions to answer - I actually found it because I was hoping someone had the question "How do we know the normal PDF is a PDF?" and I searched for it. But I think the answer to the question may be to demonstrate the origin of the normal distribution.

The normal distribution was first designed to be used to approximate the binomial distribution for very large $n$. In 1744, a mathematician named De Moivre showed that the binomial distribution, for large $n$, has very similar probabilities to a normal distribution with mean $np$ and variance $np(1-p)$. The proof of this follows pretty naturally from taking the limit of the binomial pdf as $n\to\infty$, and replacing the factorial values with Stirling's approximation.

But I am again tempted to get very deep into the proof that this happens, and I don't know that is what the OP wanted. If interested, it is explained here. Just know that we can "easily" prove that the limit of the binomial distribution as $n\to\infty$ and $p\to0$ such that $np=1$ is a normal distribution.

Taking that knowledge, we can see why the normal distribution is bell shaped if we can see why the binomial distribution is bell shaped, which is much easier to see. Go ahead and try it for yourself - make a discrete graph of the binomial probabilities for $n=10$ and $p=0.5$. How is it shaped? What about a discrete graph of the binomial probabilities for $n=100$ and $p=0.5$? Indeed, do it empirically, generate some random data distributed Binomially and see how the histogram looks! Of course, it's a pretty blocky looking bell, but it gets more curvy the higher $n$ is. But why is it bell-shaped at all?

If I dump 100 coins on the ground right now and count how many heads I get, I might count 0 heads, or I might count 100 heads, but I'm way more likely to count a number somewhere in between. Do you see why this histogram should be bell shaped?

birdsoong
  • 31
  • 1
  • +1 -- however, note that I discuss de Moivre in several parts of my answer. You may find the final note in my answer in relation to discrepancies in the references interesting - it's worth actually looking at what de Moivre wrote to see the extent to which the different characterizations of his work seem to hold up. Specific discussion about why the binomial cdf becomes well approximated by a normal cdf under suitable conditions is discussed in [Why is a binomial distribution bell-shaped?](https://stats.stackexchange.com/questions/176425/why-is-a-binomial-distribution-bell-shaped/176428) – Glen_b Sep 28 '17 at 00:55
1

Would also mention Maxwell-Herschel derivation of independent multivariate normal distribution from two assumptions:

  1. Distribution is not affected by rotation of the vector.

  2. Components of the vector are independent.

Here is the exposition by Jaynes

Roah
  • 285
  • 1
  • 6