How is the $\chi^2_1$-distribution not a Gaussian?

Question

The $\chi ^2_n$-distro is the distribution of the sum $Z_1 ^2+Z_2 ^2+...$ where the $Z_i$ are drown from a standard normal distribution.

However, the standard normal distribution is a Gaussian bell curve, i.e. $\frac{1}{\sqrt{2\pi}}exp(-\frac{x^2}{2})$

so squaring this would give another bell curve:

$\frac{1}{2\pi}exp(-x^2)$.

So why, then, is this not the $\chi^2_1$-distribution?

Is a random variable the same thing as its probability density function? — Sycorax, Jul 27 '16 at 15:11

score 13 · Answer 1 · edited Apr 13 '17 at 12:44

13

Normally distributed random variable can take values ranging from $-\infty$ to $\infty$. Squaring any real value would lead to positive values. So how can possibly $Z^2$ be normally distributed?

Squaring probability density function does not make any sense since this would give you "probabilities squared" (more precisely: squared density) rather then squared random variable. Applying any function $g$ to random variable $X$ means applying it to $X$'s values rather then to it's probability density function, or cumulative distribution function.

edited Apr 13 '17 at 12:44

Community

1

answered Jul 27 '16 at 15:08

Tim

108,699
20
212
390

6

This explains why a normal distribution can't be correct. But it would also be worth directly addressing the faulty reasoning in the question - that squaring a RV doesn't mean just squaring the PDF. – Silverfish Jul 27 '16 at 15:09
@Silverfish that's actually what I was hoping for. – AlphaOmega Jul 27 '16 at 15:13
1

@Silverfish, this is a direct reasoning, or counter reasoning. It shows that the square of variable is not a square of the distribution PDF – Aksakal Jul 27 '16 at 15:25

TrynnaDoStat · Accepted Answer · 2016-07-27T17:47:55.423

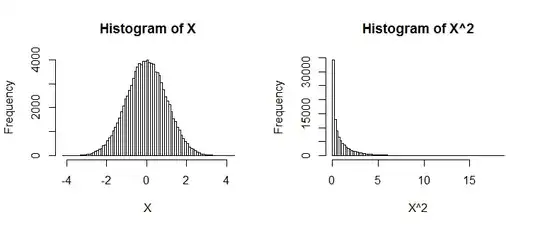
As Silverfish said, the problem in your reasoning is that to find the PDF of a squared random variable, or any other transformed random variable, you can't just perform that transformation on the PDF.

If we want to know the actual PDF of a squared random variable we must calculate $P(\chi ^2_1 = x)$. One way to do this is to use the CDF method below,

$P(\chi ^2_1 \leq x) = P(Z^2 \leq x) = P(-\sqrt{x} \leq Z \leq \sqrt{x}) = P(Z \leq \sqrt{x}) - P(Z \leq -\sqrt{x})$

Since the derivative of the CDF is the PDF, we take the derivative of both sides with respect to $x$ and get,

$f_{\chi ^2_1}(x) = \frac{1}{2\sqrt{x}} f_Z(\sqrt{x}) + \frac{1}{2\sqrt{x}}f_Z(-\sqrt{x}) = \frac{1}{2\sqrt{x}} \frac{1}{\sqrt{2\pi}}e^{-x/2} + \frac{1}{2\sqrt{x}} \frac{1}{\sqrt{2\pi}}e^{-x/2} = \frac{1}{\sqrt{x}}\frac{1}{\sqrt{2\pi}}e^{-x/2}$

which is the PDF we expect for a Chi-square distribution with one degree of freedom.

(+1) The notation $P(Z = \sqrt{x})$ is a little weird to me, my brain says, "shouldn't that be zero"? Maybe introducing a small notation for the pdf and cdf, say $\phi$ and $\Phi$ would be even clearer. — Matthew Drury, Jul 27 '16 at 17:40

Aksakal · Answer 3 · 2016-07-27T15:41:19.870

Actually, $\chi^2_\infty$ distribution "looks like" normal. The exact relation for $x\sim\chi^2_n$ is $(x-n)/2\sqrt n\sim\mathcal{N}(0,1)$

How come? As you noted a variable from this distribution can be thought of as a sum of squared normals: $Z_1^2+Z_2^2+\dots+Z_n^2$. However, the squared normal random variables are themselves random variables, albeit not normal anymore. We also know from CLT, that a sum of random variables must converge to some kind of a normal variable.

Also, you proposed to square the normal PDF to get the PDF of the square of normal variable. That doesn't work. For instance, if you take an integral of your new proposed PDF, you get $\frac{1}{2\sqrt \pi}$ instead of 1. So, the squared PDF of normal distribution is not even a PDF, it doesn't normalize to 1.

How is the $\chi^2_1$-distribution not a Gaussian?

3 Answers3