Multivariate time series clustering

Question

I am collecting a group of multivariate time sequences. For example, there are 2000 time series. Each time series is of 12 dimensions.

Are there any systematic models/algorithms that can cluster multivariate time series? For instance, I would like to identify some time series that are very different with others.

Moreover, for the online monitoring, I may run this algorithm in an on-time fashion. For instance, every 10 minutes, I run this kind of algorithm against the time series covering 10 minutes. Are there any efficient algorithms with respect to this?

Answer 1

The R package pdc offers clustering for multivariate time series. Permutation Distribution Clustering is a complexity-based dissimilarity measure for time series. If you can assume that differences in time series are due to differences w.r.t. complexity and, specifically not due to differences in means, variances, or the moments in general, this may be a valid approach. The algorithmic time complexity of calculating the pdc representation of a multivariate time series is in O(DTN) with D being the number of dimensions, T being the length of the time series and N being the number of time series. This is probably as efficient as it gets since a single sweep over each dimension of each time series is enough to obtain the compressed complexity representation. This representation can be used to calculate dissimilarity between two time series at low cost (depending on the chosen representational complexity which can either be pre-specified or derived from the data).

Here is a simple worked example with a hierarchical clustering of multivariate white-noise time series (the plot illustrates only the first dimension of each time series):

require("pdc")

num.ts <- 20 # number of time series
num.dim <- 12 # number of dimensions
len.ts <- 600*10 # number of time series

# generate Gaussian white noise
data <- array(dim = c(len.ts, num.ts, num.dim),data = rnorm(num.ts*num.dim*len.ts))

# obtain clustering with embedding dimension of 5
pdc <- pdclust(X = data, m=5,t=1)

# plot hierarchical clustering
plot(pdc)

The command pdcDist(data) generates a dissimilarity matrix:

Since the data are all white noise, there is no apparent structure in the dissimilarity matrix.

         1        2        3        4        5        6        7
2 4.832894                                                      
3 4.810718 4.790286                                             
4 4.812738 4.796530 4.809482                                    
5 4.798458 4.772756 4.751079 4.786206                           
6 4.812076 4.793027 4.798996 4.758193 4.751691                  
7 4.786515 4.771505 4.754735 4.837236 4.775775 4.794706         
8 4.808709 4.832403 4.722993 4.781267 4.784397 4.776600 4.787757

For more information refer to:

Brandmaier, A. M. (2015). pdc: An R package for complexity-based clustering of time series. Journal of Statistical Software, 67. doi:10.18637/jss.v067.i05 (Full text)

Answer 2

Check RTEFC ("Real Time Exponential Filter Clustering") or RTMAC ("Real Time Moving Average Clustering), which are efficient, simple real-time variants of K-means, suited for real time use when prototype clustering is appropriate. They cluster sequences of vectors. See https://gregstanleyandassociates.com/whitepapers/BDAC/Clustering/clustering.htm and the associated material on representing multivariate time series as one larger vector at each time step (the representation for "BDAC"), with a sliding time window. Pictorially,

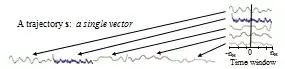
These were developed to simultaneously accomplish both filtering of noise and clustering in real time to recognize and track different conditions. RTMAC limits memory growth by retaining the most recent observations close to a given cluster. RTEFC only retains the centroids from one time step to the next, which is enough for many applications. Pictorially, RTEFC looks like:

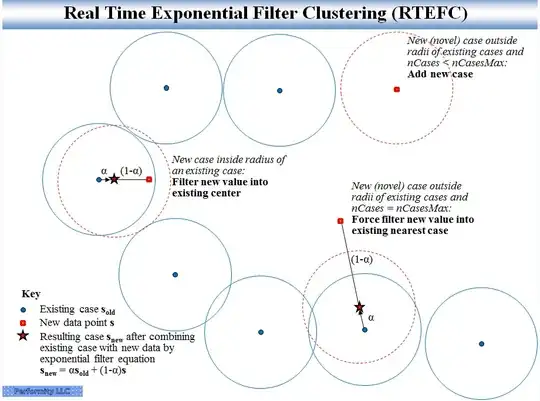
Dawg asked to compare this to HDBSCAN, in particular the approximate_predict() function. The major difference is that HDBSCAN is still assuming there is occasional retraining from original data points, an expensive operation. The HDBSCAN approximate_predict() function is used to get a quick cluster assignment for new data without retraining. In the RTEFC case, there is never any large retraining computation, because the original data points are not stored. Instead, only the cluster centers are stored. Each new data point updates only one cluster center (either creating a new one if needed and within the specified upper limit on the number of clusters, or updating one previous center). The computational cost at each step is low and predictable. So RTEFC computation would be comparable to the approximate_predict() case in finding the closest existing match, except that additionally, one cluster center is then updated with the simple filter equation (or created).

The pictures have some similarities, except the HDBSCAN picture wouldn't have the starred point indicating a recomputed cluster center for a new data point near an existing cluster, and the HDBSCAN picture would reject the new cluster case or the forced update case as outliers.

RTEFC is also optionally modified when causality is known a priori (when systems have defined inputs and outputs). The same system inputs (and initial conditions for dynamic systems) should produce the same system outputs. They don't because of noise or system changes. In that case, any distance metric used for clustering is modified to only account for closeness of the system inputs & initial conditions. So, because of the linear combination of repeated cases, noise is partly canceled, and slow adaptation to system changes occurs. The centroids are actually better representations of typical system behavior than any particular data point, because of the noise reduction.

Another difference is that all that has been developed for RTEFC is just the core algorithm. It's simple enough to implement with just a few lines of code, that is fast and with predictable maximum computation time at each step. This differs from an entire facility with lots of options. Those sorts of things are reasonable extensions. Outlier rejection, for instance, could simply require that after some time, points outside the defined distance to an existing cluster center be ignored rather than used to create new clusters or update the nearest cluster.

The goals of RTEFC are to end up with a set of representative points defining the possible behavior of an observed system, adapt to system changes over time, and optionally reduce the effect of noise in repeated cases with known causality. It's not to maintain all the original data, some of which may become obsolete as the observed system changes over time. This minimizes storage requirements as well as computing time. This set of characteristics (cluster centers as representative points are all that's needed, adaptation over time, predictable and low computation time) won't fit all applications. This could be applied to maintaining online training data sets for batch-oriented clustering, neural net function approximation models, or other scheme for analysis or model building. Example applications could include fault detection/diagnosis; process control; or other places where models can be created from the representative points or behavior just interpolated between those points. The systems being observed would be ones described mostly by a set of continuous variables, that might otherwise require modeling with algebraic equations and/or time series models (including difference equations/differential equations), as well as inequality constraints.