In this What's wrong to fit periodic data with polynomials? post, I tried to use Fourier basis expansion and Polynomial basis expansion to fit a toy periodic data (daily temperature data set). I got excellent answer from @Cliff AB and @Aksakal on why the Fourier basis is better for such case.
At the same time, @whuber mentioned in the comment, using periodic version of splines is another option. So, what are periodic version of splines and what's the basis expansion looks like?
The Venables Ripley book discusses periodic splines. Basically, by specifying (correctly) the periodicity, the data are aggregated into replications over a period and splines are fit to interpolate the trend. For instance, using the AirPassengers dataset from R to model flight trends, I might use a categorical fixed effect for annual effects and a spline to interpolate the residual monthly trends. My spline interpolation is arguably a bad one, but finding a good fitting spline is another topic altogether :) This example is perhaps a bit more useful because it deals with averaging out other auto-regressive trends.
My from-scratch method fits the periodic spline with a discontinuity at the end-point, but one could easily address this by duplicating these data over two periods and fitting the spline to the central half.
matplot(matrix(log(AirPassengers), ncol=12), type='l', axes=F, ylab='log(Passengers)', xlab='Month')
axis(1, at=1:12, labels=month.abb)
axis(2)
box()
title('Monthly air passenger data 1949:1960')
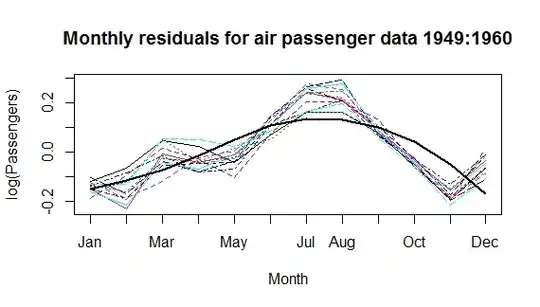
ap <- data.frame('lflights'= log(c(AirPassengers)), month=month.abb, year=rep(1949:1960, each=12))
ap$month.n <- match(ap$month, month.abb)
ap$monthly.diff <- lm(lflights ~ factor(year), data=ap)$residuals
matplot(matrix(ap$monthly.diff, ncol=12), type='l', axes=F, ylab='log(Passengers)', xlab='Month')
axis(1, at=1:12, labels=month.abb)
axis(2)
box()
title('Monthly residuals for air passenger data 1949:1960')
library(splines)
ap$monthly.pred <- lm(monthly.diff~bs(month.n, degree=2, knots = c(5)), data=ap)$fitted
lines(1:12, ap$monthly.pred[1:12], lwd=2)
