Parameter estimation of a Rayleigh random variable with an offset

Question

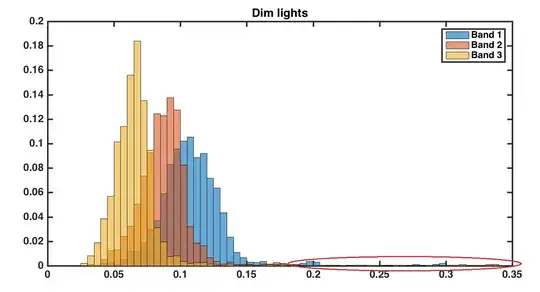
I have data that is believed to be Rayleigh distributed (according to some academic papers). However, when I plot the histogram (probability normalized below) it looks like a Rayleigh distribution with an offset. Is there a way to "standardize" such a random variable so I can fit a Rayleigh parameter to it? I am thinking of when we take Normal RV's and subtract the mean and divide by the variance to make it standard (zero mean, unit variance). If that doesn't sound like a correct thing to do, is there a similar distribution that has a parameter for this kind of shift?

Answer 1

One important thing to note is that your data don't appear to be consistent with having been drawn from a Rayleigh population -- the right tail is considerably too heavy.

Nevertheless, I'll continue as if the shifted-Rayleigh were a suitable model.

---

If the offset is unknown you can estimate it as a parameter.

The density for a one-parameter Rayleigh is:

$\qquad f(x;\sigma )={\frac {x}{\sigma ^{2}}}e^{-x^{2}/(2\sigma ^{2})},\quad x\geq 0,$

If we introduce a shift $\mu$, it becomes:

$\qquad f(x;\mu,\sigma )={\frac {x-\mu}{\sigma ^{2}}}e^{-(x-\mu)^{2}/(2\sigma ^{2})},\quad x\geq \mu .$

[NB Here $\mu$ is the lower bound on the random variable, not the mean.]

Dey et al, 2014 [1] discuss estimation in the two-parameter Rayleigh case. (However, you should carefully note that in the parameterization there, the second parameter, $\lambda$, is not the scale - even though they say it is - in fact, $\sigma$ (or anything proportional to it) is a scale parameter, where $\lambda=(2\sigma^2)^{-1}$.)

They provide a simple iterative estimator for the MLE of the shift parameter, $\mu$: $\require{enclose}$ $${\mu}^{[j+1]}=\enclose{horizontalstrike}{2\sum_{i=1}^n(x_i-\mu^{[j]})^2\times \sum_{i=1}^n(x_i-\mu^{[j]})\times \sum_{i=1}^n(x_i-\mu^{[j]})^{-1}}$$

[Edit: It looks like this formula (found in both the working and published versions!) cannot be correct, since it's in squared units-of-$x$. Clearly a shift/location parameter has to be in units-of-$x$.

For the moment (until I see if I can derive it correctly myself), probably the best thing to do is optimize the profile log likelihood for $\mu$ in equation 7 using a univariate optimizer:

$\qquad g(\mu) = \sum_{i=1}^n\ln\left[\frac{(x_i-\mu)}{\sum_{i=1}^n(x_i-\mu)^2}\right]$

• a quick check of the algebra seems to suggest this formula is correct up to an additive constant. Running a few dozen examples on randomly generated Rayleigh data - both in small (n=10) and moderately large samples (n=1000) - suggests that simply optimizing the profile log likelihood directly seems to work quite well. I used Brent's method but any number of reasonable optimization methods should work adequately.]

Then $\hat{\mu}$ is taken to be the value of ${\mu}$ at the last iterate obtained at convergence, ${\mu}^{[T]}$, say.

These iterations could be started (${\mu}^{[0]}$) at the method of moments estimator of $\mu, \tilde{\mu}=\bar{x}-k s$ where $\bar{x}$ and $s$ are the sample mean and standard deviation respectively, and $k = \frac{\Gamma(\frac32)}{\sqrt{1-\Gamma(\frac32)^2}}=\sqrt{\frac{\pi}{4-\pi}}\approx 1.913$, or at some suitably small distance below the smallest observation (e.g. ${\mu}^{[0]}=x_{(1)}-\frac{c}{\sqrt{n}}$ with $c$ near $0.3$ should work reasonably well as a start point). Note that the method of moments estimator may sometimes exceed the smallest observation (and should be avoided/modified in that case).

If the data are then shifted by $\hat{\mu}$, $x^{(0)}_i=x_i-\hat{\mu}$, the scale parameter may be estimated from the back-shifted data in the usual fashion for a Rayleigh distribution. Standard errors and confidence intervals follow in the same fashion.

Interestingly, (but not entirely surprisingly for a shift parameter on a random variable bounded below by it), the shift parameter doesn't have the "usual" asymptotics for MLEs, in that the variance isn't proportional to $\frac{1}{n}$.

(The paper gives asymptotic confidence intervals for the parameters - but again, note that they don't use the same parameterization for the main parameter. The same paper discusses other estimators, but since the MLEs are fairly simple, I'd suggest sticking with them)

[1]: Dey, S., T. Dey, and D. Kundu (2014),
Two-Parameter Rayleigh Distribution: Different Methods of Estimation,
American Journal of Mathematical and Management Sciences, Vol 33, No 1, p55-74
(working paper here)