I'm trying to understand the $\chi^2$-distribution. Wikipedia has the following graph for the probability density function:
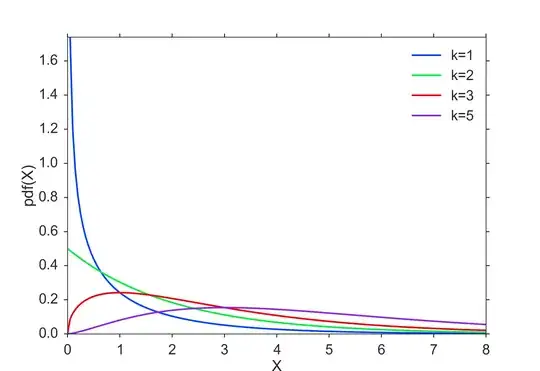
This graph shows that for $ k = 1$, the PDF will be... infinite? The mode of the $\chi^2$-distribution is defined as $max \{k − 2, 0\}$, so $f_1(0) = ?$
In other graphs on the Web, it seemed like it even went higher than $1$. Like here:
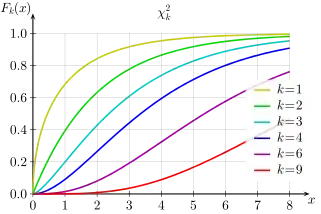
Of course, the cumulative distribution function approaches $1$ for all degrees of freedom:
I don't understand why the probability distribution function behaves like that around $0$ for any $k$. How is the $\chi^2$-distribution defined around $0$?