8

Consider a typical 2x2 table of frequencies (shown in this image):
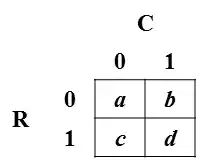
two by two table
Notation: The row variable is denoted R and takes on values 0 or 1; the column variable is denoted C and takes on values 0 or 1. The cells of the table indicate the frequency of each combination of R and C; for example, $b$ is the frequency of R=0 and C=1. For purposes of my question, assume that the cell counts are divided by the total, so that the cell values are the joint probabilities of the cells.

I want to express the cell probabilities in terms of the phi coefficient (which is a measure of correlation with formula provided below) and the marginal probabilities: $\mu_R\equiv p(R\!=\!1) = c+d$ and $\mu_C\equiv p(C\!=\!1) = b+d$. That is, I want to invert the following system of four equations: $$\begin{align} \phi &\equiv (ad-bc)/\sqrt{(a+b)(c+d)(a+c)(b+d)} \tag{by defn}\\ \mu_{R} &= c+d \tag{by defn}\\ \mu_{C} &= b+d \tag{by defn}\\ 1 &= a+b+c+d \tag{constraint} \end{align}$$ and, of course, $0 \le a,b,c,d \le 1$. In other words, I would like to solve for $a$, $b$, $c$, and $d$ in terms of $\phi$, $\mu_{R}$, and $\mu_{C}$.

This problem has probably been solved by somebody before, but my searches have not yielded a source, and my feeble attempts at algebra have not produced an answer, and I cannot find online system-of-(nonlinear)-equation inverters that handle this case.

John K. Kruschke
  • 2,153
  • 12
  • 16

1 Answers1

4

We easily recognize every factor in the denominator of $\phi$, because $a+b=1-\mu_R$ and $a+c=1-\mu_C$. Let's therefore start with a tiny simplification to avoid writing lots of square roots:

$$\Delta=ad - bc = \phi \sqrt{\mu_R(1-\mu_R)\mu_C(1-\mu_C)}.$$

Let's find $d$:

$$\eqalign{d &= (1)d = (a+b+c+d)d = ad +bd +cd + d^2 \\ &= ad + (-bc + bc) + bd + cd + d^2 \\ &= (ad - bc) + (c+d)(b+d) \\&= \Delta + \mu_R\mu_C.}$$

Finding $a$, $b$, and $c$ proceeds similarly due to the symmetries of the problem: interchanging the columns swaps $a$ and $b$, $c$ and $d$, while changing $\mu_C$ to $1-\mu_C$ and negating $\Delta$, whence $$c = -\Delta + \mu_R(1-\mu_C).$$

Interchanging the rows swaps $a$ and $c$, $b$ and $d$, while changing $\mu_R$ to $1-\mu_R$ and negating $\Delta$, whence

$$b = -\Delta + (1-\mu_R)\mu_C.$$

Swapping both rows and columns yields

$$a = \Delta + (1-\mu_R)(1-\mu_C).$$

Given these expressions for $a,b,c,d$, it is simple to check that $a+b+c+d=1, c+d=\mu_R,$ and $b+d=\mu_C$, and only a little bit harder to verify that $ad-bc=\Delta$.

whuber
  • 281,159
  • 54
  • 637
  • 1,101
  • One note to others who might use this (correct!) answer: It can yield values of a, b, c, or d that are negative. In other words, not all combinations of phi in [-1,1], mu_R in [0,1], and mu_C in [0,1] can be created by probability matrices. To whuber: Thank you! – John K. Kruschke Jul 14 '16 at 12:01
  • That's correct, John, but I made no mention of that fact because presumably $\mu_R$, $\mu_C$, and $\phi$ had been obtained from a valid table in the first place. Assuming $\mu_R$ and $\mu_C$ are valid frequencies (in the interval $[0,1]$), $\Delta$ will be real. It must lie in the interval $$[-\min(\mu_R\mu_C, (1-\mu_R)(1-\mu_C)), \ \min(\mu_R(1-\mu_C), (1-\mu_R)\mu_C)].$$ – whuber Jul 14 '16 at 13:16