Comparing silhouette scores between different datasets (having different number of variables)

Question

Full Question

Experiment 1 clustered data using variables X and Y. Experiment 2 clustered data using variables X, Y and Z (i.e. a third variable was added).

Would it be valid to compare silhouette scores between cluster results in experiments 1 and 2 to say that one experiment of the two produced better results than the other - because it showed a higher silhouette score?

TL:DR

Is it valid to compare the silhouette scores of two clustering results, if the two different experiments used slightly different data? Such as different number of variables.

Answer 1

Be careful!

Consider the case where you compare the data set $(X,Y)$ to one where you added some noise to copies of the attribute, i.e. $(X,Y,X+\epsilon_1,Y+\epsilon_2)$.

Then evaluate the exact same clustering (i.e. computed on $(X,Y)$) on this noisier version. It will perform worse. Add more dimensions like this, and it may eventually become really bad.

Additional variables are expected to reduce silhouette, so comparison is biased towards the smaller data set. The reason is simple: there is more variation to account for.

But if your result actually improves with the additional data, then either the additional attribute helped, or it just is of higher magnitude, and the silhouette of clustering $(Z)$ alone would be even better... (Normalization is extremely important. Try different ways of normalizing/standardizing your data, and different distance functions, and you will get very different results!)

Answer 2

Short Answer: Yes

Long Answer: Clustering Scores are being used to compare how "well" a data-set is clustered. Usually you use such scores to tune the parameters of your clustering algorithm. For example you can run k-means for different k and based on the evaluation score choose the right one for your dataset. As you asked, you can also use the score the compare different clustering approaches, for example, clustering based on different attributes.

If you could provide some more information on your problem I might have something more specific.

Take a look at the following topic for more clustering evaluation methods and ideas that might help you. Evaluation measure of clustering

Answer 3

Silhouette clustering index has the general formula $\frac{b-a}{\max(b,a)}$, where $a$ is the distance from a point to its cluster (where it is clustered) and $b$ is the distance from the point to another cluster, "second close" to the point. The index computes for each data point and the mean index across all data points is considered the ovrall quality of the cluster partition.

Let us question the dependency of the ratio lying in the formula on the dimensionality of dataset. We'll not be doing cluster analysis nor considering any point groupings. Instead, we'll consider all triples of individual points in a random one-cloud data (i.e. data generated as having no clusters, where "clusters" could occure as a random coincidence).

Generate n points by p variables random uncorrelated data from standard normal or from standard uniform distribution. Compute n by n matrix of eucliclidean distances between the points. Consider every triplet of points and compute $\frac{b-a}{b}$ where $a$ is the smallest of the three distances in the triplet and $b$ is the next smallest of the three. (As we are not doing real clustering, let us fashion an "ideal cluster solution" scenario by assuming that a point is always closer to its cluster than to an alien cluster, and that the distance between the two clusters is futher larger because the "alien" cluster is a one which is actually enough close to our point.) Compute mean of such ratio over all the triplets. Repeat the whole task (simulation/computation) number of times. Observe the overall mean ratio and its variation.

Results for n = 30, 10 simulations in two distributions. The mean and st. deviation of the ratio for dimensionality p = 1 through 6:

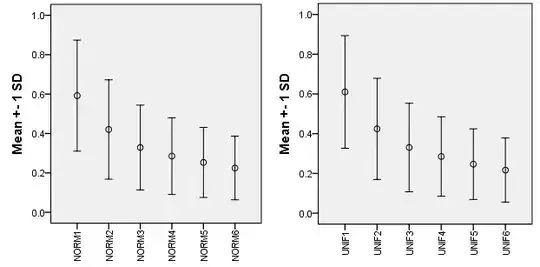
The ratio clearly depends on the dimensionality. It stabilizes asymptotically in the perspective of large p. I conclude that one should mind when directly comparing Silhouette clustering index values obtained for datasets with different number of variables p1 <> p2; especially when min(p1,p2) is small one should refrain to compare.