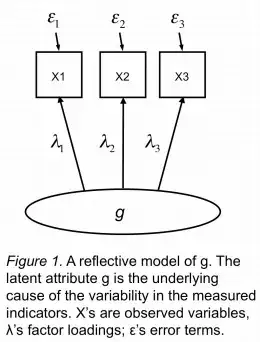
In the sorts of measurement models to which one might apply IRT models, including Rasch models, there is not thought to be an error associated with the latent variable. Rather, the latent variable is thought to cause indicators, which themselves have uncorrelated errors (see below).
What I'm wondering though is about the consequences of violating these assumptions. For example, if I apply an IRT/Rasch model to data where the latent variable possesses error, and the indicators do not possess local independence, does this bias the results (or render them meaningless) or are these methods robust to the violations?
I'm asking because I work in a field where people routinely apply models of these sorts to data which seem likely to violate the assumptions. This is done, for example, to determine whether items in an assessment should be retained or removed. Furthermore, there appears an assumption that being able to fit such a model to data generated by an assessment is a reflection on the quality of the assessment.
Image source:
@article{kievit2011mind,
title={Mind the gap: a psychometric approach to the reduction problem},
author={Kievit, Rogier A and Romeijn, Jan-Willem and Waldorp, Lourens J and Wicherts, Jelte M and Scholte, H Steven and Borsboom, Denny},
journal={Psychological Inquiry},
volume={22},
number={2},
pages={67--87},
year={2011},
publisher={Taylor \& Francis}
}