5

I understand that ReLUs are used in Neural Nets generally instead of sigmoid activation functions for the hidden layer. However, many commonly used ReLUs are not differentiable at zero. Gradient Descent (Stochastic or Batch) is quite often used to optimize these.

GD needs functions to be smooth and continuous. So I'm confused on how do ReLUs still work in the context of using GD for finding the global minima?

HakunaMaData
  • 153
  • 5

1 Answers1

10

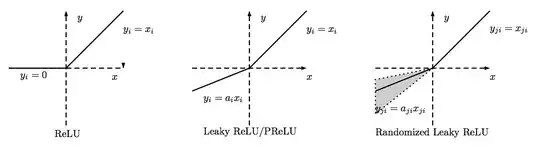
In practice, it's unlikely that one hidden unit has an input of precisely 0, so it doesn't matter much whether you take 0 or 1 for gradient in that situation. E.g. Theano considers that the gradient at 0 is 0. Tensorflow's playground does the same:

public static RELU: ActivationFunction = {
    output: x => Math.max(0, x),
    der: x => x <= 0 ? 0 : 1
  };

(1) did notice the theoretical issue of non-differentiability:

This paper shows that rectifying neurons are an even better model of biological neurons and yield equal or better performance than hyperbolic tangent networks in spite of the hard non-linearity and non-differentiability at zero, creating sparse representations with true zeros, which seem remarkably suitable for naturally sparse data.

but it works anyway.

As a side note, if you use ReLU, you should watch for dead units in the network (= units that never activate). If you see to many dead units as you train your network, you might want to consider switching to leaky ReLU.

enter image description here

Community
  • 1
Franck Dernoncourt
  • 42,093
  • 30
  • 155
  • 271
  • +1. When using theano, the gradient of the relu activation function at 0 depends on how the function is implemented. The linked stackoverflow post uses a `switch` statement. Using the builtin `theano.nnet.relu` gives a gradient value of 0.5 at 0. Of course, it makes little practical difference, as you mentioned. – user20160 Jul 07 '16 at 06:44
  • @Sycorax sure see http://stats.stackexchange.com/a/229015/12359 – Franck Dernoncourt Sep 19 '16 at 14:55