2

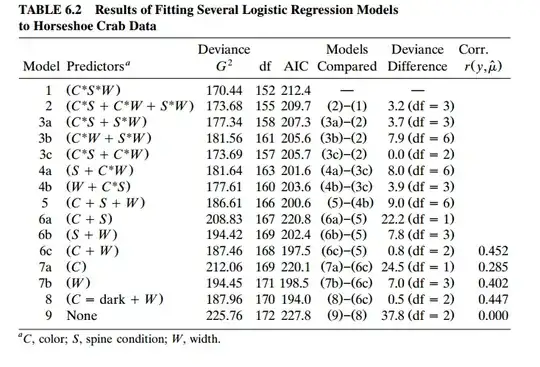
I'm having trouble to understand Backward elimination in Logistic Regression model. I was looking at this example of Agresti, Categorical Data Analysis, to see how Backward elimination works.

enter image description here

What I understood is:

In the Backward elimination, we first built the full model with all independent variables and interactions. Then we start to look at the interactions of high order,checking whether they are significant or not, and eliminating them.

Let $M_1$ the model $1$ and $M_2$ the model $2$, so to test if the interactions of $order=3$ are significant we test the hypothesis $$H_0:M_2\ is\ the\ true\ model$$ where $$Deviance(M_2)-Deviance(M_1)\sim \chi_3^2$$

Since $Deviance(M_2)-Deviance(M_1)=3.2$ and $p.value=0.36$ we don't reject $H_0$. Then $M_2$ is true and the interactions of $order=3$ are insignificant.

That is the idea? If I already tested all interactions, I can apply the same criterion for the main effects to test if they are significant?

How the AIC criterion works? In this case is better choose the model 8 because that have the smallest AIC?

I read in different places, but I still don't understand well. How can I choose the better method of variable selection?

1 Answers1

4

It is not possible to test whether a model is 'true' or not with hypothesis testing. Null hypothesis here would be better verbalized as "There is no difference between the fit of model 1 and model 2." If it is not rejected, it is reasonable to choose the simpler model.

How AIC works is explained by Agresti in the following section in the book. I'd suggest you read it as it seems to answer the questions you have posed above. Briefly, yes, the smaller the AIC the better.

There wouldn't be a straight forward answer for your last question that would hold in general. However, it seems that you are considering to come to a conclusion about this matter and carry that information on. I think it may be useful to direct your attention to a cautionary note about variable selection in general:

Hypothesis testing as is applied commonly does not take the model selection procedure into account. Hence if you build several models and pick one of them based on a certain criteria and move on to use hypothesis testing without taking this procedure into account, you are more likely to err than not. Chatfield (1995) outlines some of the problems as follows (there is a good deal of detail in the paper, would be useful as well):

  1. Least squares theory does not apply when the same data are formulated and fit a model.
  2. After model selection, estimates of the model parameters and residual variance are likely to be biased.
  3. The analyst typically thinks that the fit is better than it really is and diagnostic checks rarely reject the best fitting model.
  4. Prediction intervals are generally too narrow.
Ozan Öğreden
  • 186
  • 6