Why are points uniformly distributed on a sphere in 3D uniformly distributed in component coordinates?

Question

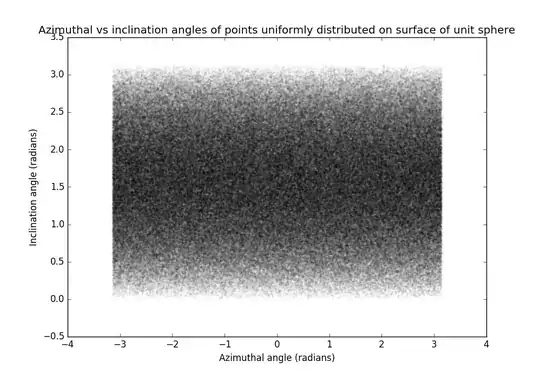
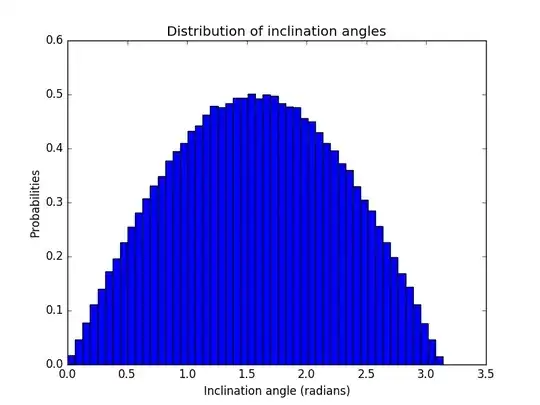
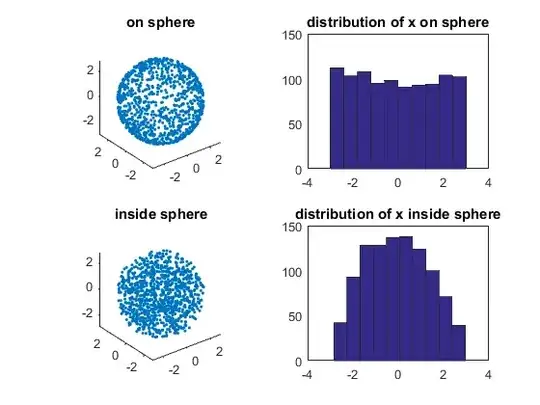
I've generated uniformly random points on a sphere (in 3D). As expected, all azimuthal angles are drawn with equal probability and it's less likely to draw points close to the poles:

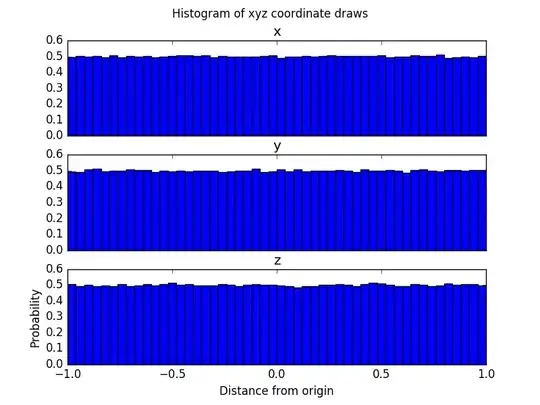
However, when I histogram the Cartesian coordinates, I see that the draws are uniformly distributed in all dimensions:

Why are the points uniformly distributed in the x, y, and z dimensions? I don't find that intuitive. Slices near the poles have less surface area than slices near the equator. Therefore, I expect more points on the equatorial slice, and for the points to cluster around the mean when I project them onto a single dimension (like the distribution of theta):

I generated uniformly random points on the surface of the sphere with 3 different methods because I was convinced I was doing something wrong, but they all gave the same results:

import numpy as np
from numpy.random import uniform

n = 500000

# python implementation of http://stackoverflow.com/a/6390021/4212158
# where theta0 => azimuth and theta1 => inclination
azimuth = uniform(0, 2*np.pi, n)
inclination = np.arccos(1 - 2*uniform(0, 1, n))
radius = 1.
x = radius * np.sin(inclination) * np.sin(azimuth)
y = radius * np.sin(inclination) * np.cos(azimuth)
z = radius * np.cos(inclination)

# rescaling draws from 3D gaussian method
# credit http://stackoverflow.com/a/33977530/4212158
gaussian_points = np.random.randn(3, n)
x, y, z = gaussian_points / np.linalg.norm(gaussian_points, axis=0)
azimuth = np.arctan2(y, x)
inclination = np.arccos(z)

# trig method 2
# credit http://stackoverflow.com/a/14805715/4212158
z = uniform(-1, 1, n)
azimuth = uniform(0, 2*np.pi, n)
x = np.sqrt(1 - z**2) * np.cos(t)
y = np.sqrt(1 - z**2) * np.sin(t)
inclination = np.arccos(z)

Python code for the plots:

import matplotlib.pyplot as plt
f, axarr = plt.subplots(3, sharex=True)
axarr[0].hist(x, bins=50, normed=True)
axarr[0].set_title('x')
axarr[1].hist(y, bins=50, normed=True)
axarr[1].set_title('y')
axarr[2].hist(z, bins=50, normed=True)
axarr[2].set_title('z')
plt.suptitle('Histogram of xyz coordinate draws')
plt.xlabel("Distance from origin")
plt.ylabel("Probability")
plt.show()


fig3 = plt.figure()
plt.scatter(azimuth, inclination, c='black', marker='.', alpha=.02)
plt.title("Azimuthal vs inclination angles of points uniformly distributed on surface of unit sphere")
plt.xlabel("Azimuthal angle (radians)")
plt.ylabel("Inclination angle (radians)")
plt.show()

fig = plt.plot()
plt.hist(inclination, bins=50, normed=True)
plt.title("Distribution of inclination angles")
plt.xlabel("Inclination angle (radians)")
plt.ylabel("Probabilities")
plt.show()

I call this the "tennis can theorem." (It was known to Archimedes, but not by that name.) The total surface area of tennis balls packed tightly in a cylindrical can equals the surface area of the can itself (not counting its caps). In fact, more is true: were you to make two orthogonal slices through can and balls both, then the surface area of the can and the surface area of the ball(s) you cut out would be equal. BTW, the situation for general spheres in $\mathbb{R}^D$ is fully characterized at http://stats.stackexchange.com/questions/85916. — whuber, Jul 05 '16 at 19:26
If you were to pick points _inside_ the sphere (not _on_ it), then the cartesian cooridnate distribution would not be uniform. It would be approaching the Gaussian as the number of dimension increases, if you look at the hypersphere rather than a usual 3d sphere — Aksakal, Jul 05 '16 at 19:59
@Aksakal As the dimension increases, almost all the points inside the sphere grow extremely close to its boundary, so asymptotically the two problems are the same. BTW, in $\mathbb{R}^1$ the points inside the sphere *are* uniformly distributed. — whuber, Jul 05 '16 at 20:39
@whuber, I disagree. The inside sphere collapses into a point. while when you force the points to stay on the surface this doesn't happen. The problems are starkly different — Aksakal, Jul 05 '16 at 20:48
@Aksakal One can express the problem for the interior of the sphere as a mixture of densities on the surfaces of spheres of all radii $0 \le \rho \le 1$. The contributions to that mixture for $\rho\approx 1$ are all very similar to the density on the surface. Because the volume of a hypersphere of radius $1-e\approx 1$ in $\mathbb{R}^D$ is proportional to $(1-e)^{D-1}\approx \exp(-De)$, the contributions from smaller $\rho$ become vanishingly small as the dimension increases and therefore need no further consideration. BTW, the method of the referenced thread gives Beta$((D+1)/2,(D+1)/2)$. — whuber, Jul 05 '16 at 20:54
@whuber, I look at the interior of the sphere as a problem of stacked disks. Stacked along the Cartesian axis of interest. This approach is more natural for this problem, and intuitively makes it clear that the distribution can't be uniform, in my opinion — Aksakal, Jul 05 '16 at 21:00
@Aksakal Of course it's not uniform! It's uniform only in $\mathbb{R}^1$--but that is a sufficient counterexample to your original statement that it "would not be uniform". If you simply modify my answer to the [previously referenced thread,](http://stats.stackexchange.com/a/85977/919)--which in fact is in terms of the stacked disks--you will discover the distribution of x-coordinates within the interior of the unit sphere in $\mathbb{R}^D$ is the same as their distribution on the surface of the unit sphere in $\mathbb{R}^{D+2}$. With $D=1$ we obtain a nice answer to this question. — whuber, Jul 05 '16 at 21:03
@whuber, ok I see that I misunderstood your $R^1$ as the projection of hypersphere to $R^1$ (like in OP's question) while you actually meant the sphere in $R^1$. We're on the same page now — Aksakal, Jul 05 '16 at 21:15

Aksakal · Accepted Answer · 2016-07-05T21:18:09.280

Here's where your intuition fails you: slice the surface into rings of equal width along $x$ axes. Although the width along $x$ is the same $\Delta x$, the width of the surface of each band gradually increases as you move from $x=0$ to $x=1$, because the surface turns from horizontal to vertical. The angle change is just enough to compensate for shorter circumference of the rings closer to the poles.

Here's my crappy diagram. You see how $dx$ is the same, but $AB$ is shorter than $CD$ (because it's at angle to $x$-axis) while $AA'$ is longer than $CC'$. In the end the surface of $AB$ band ends up being the same as $CD$ band. Magic!

Let me know if you want more detail or math. It's easy to show. Also exploring the difference between picking point on a sphere and inside a sphere is very interesting. Try getting the distributions of Cartesians for the latter case.

Here's MATLAB code and plots for these two cases and 3 dimensions.

rng(0,'twister')
rvals = 2*rand(1000,1)-1;
elevation = asin(rvals);

azimuth = 2*pi*rand(1000,1);
radii = 3*(rand(1000,1).^(1/3));

[x,y,z] = sph2cart(azimuth,elevation,3);
figure
subplot(2,2,1)
plot3(x,y,z,'.')
axis equal
title 'on sphere'

subplot(2,2,2)
hist(x)
title 'distribution of x on sphere'

[x,y,z] = sph2cart(azimuth,elevation,radii);
subplot(2,2,3)
plot3(x,y,z,'.')
axis equal
title 'inside sphere'

subplot(2,2,4)
hist(x)
title 'distribution of x inside sphere'

Why are points uniformly distributed on a sphere in 3D uniformly distributed in component coordinates?

1 Answers1

Linked

Related