1

From what I understand a smooth function 1-degree is a function whose first derivative is continuous? How this helps in estimating the parameters? What if the function is not smooth?

Stephan Kolassa
  • 95,027
  • 13
  • 197
  • 357
Ajay Singh
  • 149
  • 1
  • 9

1 Answers1

6

First, the cost function does not to be smooth, and there are many widely used cost functions are not smooth. For example, the loss for least absolute deviations and support vector machine is using Hinge Loss, which is also not smooth.

Here is the comparison for least square and least absolute deviation. Least absolute deviation is widely used and more robust to outliers.

  • Least square (smooth) $L(y,\hat y)=(y-\hat y)^2$

  • Least absolute deviation(continuous but not smooth) $L(y,\hat y)=|y-\hat y|$

Second, continuous and differentiable (smooth) are good features to have in the cost function (but perfectly OK to not have). If the objective function is smooth, and we can calculate the gradient, the optimization (how to find the values for all parameters) is easier to solve.

Many solvers need gradient as an input. Intuitively, gradient tells us where to go to update parameters to get lower cost in the optimization (model fitting) process. On the other hand, there are many gradient free algorithm to do the optimization, so it is OK to have a non-smooth objective function.

In addtion, in real world, not only the objective function can be non-smooth, but also it can discretely defined. Think about 0-1 loss, which is number of mis-classifications. It is a discrete function, where

$L(y,\hat y)=$ $ \begin{cases} 0 & y=\hat y\\ 1 & y\neq\hat y \end{cases} $ If a function is a discrete function then it definitely is not smooth.

0-1 loss is hard to minimize and we are not directly using it in real world. But the reason is not because it is non-smooth but it is non-convex.

Comparing to smoothness, convexity is a more important for cost functions. A convex function is easier to solve comparing to non-convex function regardless the smoothness.

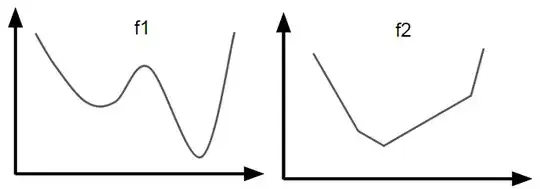
enter image description here

In this example, function 1 is non-convex and smooth, and function 2 is convex and none-smooth. Performing optimization on f2 is much easier than f1. In fact, the loss for least absolute deviations on whole data set is very similar to f2.

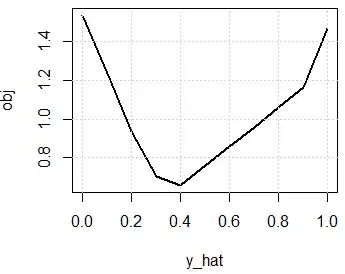
Here is code to plot the loss function on a toy data set for least absolute regression. Where in this data set, you only have 3 data points, you only have the target (no features). y_hat is your estimation, and obj is the least absolute loss in whole data.

set.seed(0)
y=runif(3)
y_hat=seq(0,1,0.1)
obj=sapply(y_hat,function(y_hat) sum(abs(y-y_hat)))
plot(y_hat,obj,type="l",lwd=2)
grid()

enter image description here

Haitao Du
  • 32,885
  • 17
  • 118
  • 213
  • i've not studied about optimizations that much, thanks for the insight. – Ajay Singh Jul 05 '16 at 13:29
  • +1 Nice answer. I wonder if OP by talking about smoothness does not refer partly to convexity. Maybe convexity could also be mentioned in your answer? – Tim Jul 05 '16 at 13:44
  • @Tim Thanks. I am new to CV and feel good about upvote by high reputation users. I am trying to find the right level for an answer. I thought about the convex earlier, and would like to add it later! – Haitao Du Jul 05 '16 at 13:54
  • Maybe you're artistically challenged, but f2 doesn't look convex to me. But yes, with some adjustments, it could be made convex and non-smooth. – Mark L. Stone Jul 06 '16 at 14:27
  • @MarkL.Stone thanks Mark, you provided many useful feedback to me, I will revise it. – Haitao Du Jul 06 '16 at 14:29
  • Actually, f2 as (currently) drawn, appears to be quasi-convex, which allows bisection to be used to find the global minimum (within the bisection starting interval). – Mark L. Stone Jul 06 '16 at 14:35
  • To learn the parameters, we tend to convert the problem of learning into an Optimization problem, now ideally we would like to optimize the number of points predicted incorrectly but instead of that we choose to optimize the loss function and since you are saying that it does not matter whether the function is smooth or not, then to get a good parameters value why don't we choose the inherently non-smooth error function to optimize, i understand it would be hard to optimize. – Ajay Singh Jul 06 '16 at 16:21
  • @AjayChoudhary I think that is a good question, you can search related questions and if necessary, you can open one, and I would like to help to edit and answer. – Haitao Du Jul 06 '16 at 16:26
  • here is a link to the question http://stats.stackexchange.com/questions/222463/why-learning-parameters-through-optimization-of-loss-function-is-preferred-over – Ajay Singh Jul 06 '16 at 16:36
  • @AjayChoudhary I revised the question and posted it [here](http://stats.stackexchange.com/questions/222585/what-are-the-impacts-of-choosing-different-loss-function-in-classfication) – Haitao Du Jul 07 '16 at 13:09