3

I am wondering about how 1x1 convolution can be used to change the dimensionality of feature maps in a residual learning network.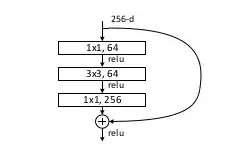enter image description here

Here the top 1x1 convolution changes the feature map size from 256 to 64. How is this possible?

In a previous post explaining 1x1 convolution in neural net, it is mentioned that, if a layer having $n_1$ feature maps is subjected to 1x1 convolution with $n_2$ filters then number of feature map changes to $n_2$. Shouldn't it be $n_1$$n_2$ since each of the $n_2$ filters produce one output corresponding to each of the $n_1$ inputs.

Also how does one generate 256 feature maps from 64, as done in the bottom layer.

Community
  • 1
Newstein
  • 398
  • 3
  • 10

1 Answers1

0

There's only one parameter for each input map in a 1*1 filter, actually the 1*1 convolution is multiplying the every element of an input map by the same scalar.

So it is similar to getting 265 linear combinations out of 64 variables, the $n$-th feature map $y_n$ is like,

$$y_n=f(w_{n,1}x_1+w_{n,2}x_2+...+w_{n,64}x_{64})$$ so actually we can get any number of output feature maps as we want. Of course if the output dimension is greater than the input dimension, the output would be redundant.

dontloo
  • 13,692
  • 7
  • 51
  • 80
  • What is $w^n_i$ ?. Is it just $w_i$ – Newstein Jul 01 '16 at 09:50
  • @Newstein It's meant to be in accordance with the subscript of $y_n$, so you have a different set of weights for different output channels. – dontloo Jul 01 '16 at 09:53
  • @Newstein I made that up, it's not in the paper. :P – dontloo Jul 01 '16 at 09:54
  • How about reducing the dimensionality from 256 to 64 in the top layer? – Newstein Jul 01 '16 at 09:58
  • @Newstein it the same, only you have n=1, 2,...,64 instead of 256. – dontloo Jul 01 '16 at 10:01
  • Are you saying that 64 $x_i$s are randomly selected from 256 input maps and their weighted combination is taken using the 64 weights ($w_i$) corresponding to the 64 1x1 filters – Newstein Jul 01 '16 at 10:07
  • @Newstein no I mean the input of course consists 256$x_i$s, and we have 256 weights per output channel, and we'll have 64 channels. – dontloo Jul 01 '16 at 10:23
  • How can we have 256 weights when there are only 64 filters? I am assuming that by weights you mean the single parameter in a 1x1 filter – Newstein Jul 01 '16 at 10:27
  • 1
    @Newstein yes by weights I mean the single parameter in a 1x1 filter, and there're not in total 64 filters, there are 64 output channels (or feature maps), which means there'll be 64*256 filters (you apply a different filter to each input channel, add up the results and apply an activation function to get the output of one channel) – dontloo Jul 01 '16 at 10:37
  • 1
    I really think this answer is misleading. There a 1x1 convolutional filter is "1x1" just in the spatial dimension, but it is a 1x1xC convolution, where C is the number of input feature maps or channels (256 for the first layer in the OPs example example). Therefore, you actually have C parameters for a 1x1 convolution. Since you want to output 64 different feature maps, you have 1x1xCx64 parameters for the whole layer. – Pepe Mandioca Feb 08 '18 at 16:47
  • 1
    @facuq yea it is, I've made some edit – dontloo Feb 09 '18 at 03:59