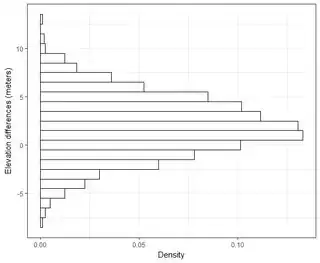
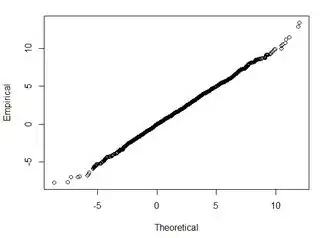
I have several datasets on the order of thousands of points. The values in each dataset are X,Y,Z referring to a coordinate in space. The Z-value represents a difference in elevation at coordinate pair (x,y).
Typically in my field of GIS, elevation error is referenced in RMSE by subtracting the ground-truth point to a measure point (LiDAR data point). Usually a minimum of 20 ground-truthing check points are used. Using this RMSE value, according to NDEP (National Digital Elevation Guidelines) and FEMA guidelines, a measure of accuracy can be computed: Accuracy = 1.96*RMSE.
This Accuracy is stated as: "The fundamental vertical accuracy is the value by which vertical accuracy can be equitably assessed and compared among datasets. Fundamental accuracy is calculated at the 95-percent confidence level as a function of vertical RMSE."
I understand that 95% of the area under a normal distribution curve lies within 1.96*std.deviation, however that does not relate to RMSE.
Generally I am asking this question: Using RMSE computed from 2-datasets, how can I relate RMSE to some sort of accuracy (i.e. 95-percent of my data points are within +/- X cm)? Also, how can I determine if my dataset is normally distributed using a test that works well with such a large dataset? What is "good enough" for a normal distribution? Should p<0.05 for all tests, or should it match the shape of a normal distribution?
I found some very good information on this topic in the following paper:
http://paulzandbergen.com/PUBLICATIONS_files/Zandbergen_TGIS_2008.pdf