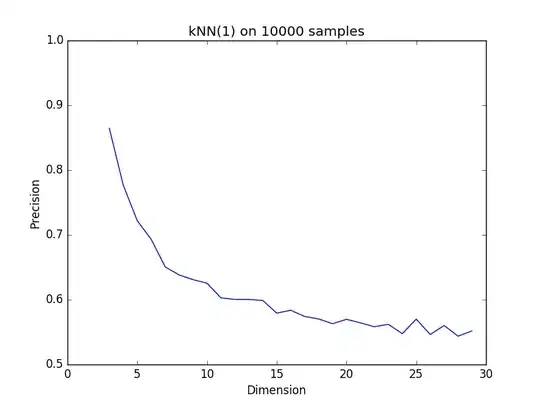
I understand what is "curse of dimensionality", and I have done some high dimensional optimization problems and know the challenge of the exponential possibilities.
However, I doubt if the "curse of dimensionality" exist in most real world data (well let's put images or videos aside for a moment, I am thinking about data such as customer demographic and purchase behavior data).
We can collect data with thousands of features but it is less likely even impossible the features can fully span a space with thousands of dimensions. This is why dimension reduction techniques are so popular.
In other words, it is very likely the data does not contain the exponential level of information, i.e., many features are highly correlated and many features satisfy 80-20 rules (many instances have same value).
In such a case, I think methods like KNN will still work reasonably well. (In most books "curse of dimensionality" says dimension > 10 could be problematic. In their demos they use uniform distribution in all dimensions, where entropy is really high. I doubt in real world this will ever happen.)
My personal experience with real data is that "curse of dimensionality" does not affect template method (such as KNN) too much and in most cases, dimensions ~100 would still work.
Is this true for other people? (I worked with real data in different industries for 5 years, never observed "all distance pairs have similar values" as described in the book.)