1

I've trained two random forests for a regression, based on the same data and variables, only with a different number of tree in each one.

If I'm not wrong, having more trees is always better in terms of how the model performs. Can you confirm that?

However, due to practical considerations, we can't afford to load a random forest of 10Gb, so we need to lower the number of trees in the forest.

How can I compare the respective performance of the forests?

Ferdi
  • 4,882
  • 7
  • 42
  • 62
François M.
  • 133
  • 2
  • 7
  • Better is a very loaded word. More trees takes longer to compute so it is not better for compute. What is your items per leaf, and max depth? How many trees are we talking about? What can you tell about the data? – EngrStudent Jun 10 '16 at 13:52
  • I mean better in terms of predictive accuracy. Items per leaf is `mtry`, right ? It's chosen by the package (`caret` and `ranger` in `R` ) using RMSE (and it's 7, there are 11 features in total). `Max depth` : I don't know (I thought that in random forest, trees went all they way to the point were one node = one data point ?). How many trees : I want to compare how well a 50 trees and a 200 trees RF do against a 500 trees RF. – François M. Jun 10 '16 at 13:59
  • I like the diagnostics and access to internal data provided by the 'h2o' and 'Flow' tools. They both come in the R library 'h2o'. You should repeat each fit some number of times and look at the distribution of errors at the end of the fit. This way you can see overlap in distribution or non-overlap in distribution. I would plot the end-error using a vioplot. – EngrStudent Jun 10 '16 at 14:36

3 Answers3

4

I like the @hxd1011 answer, and this is only to expand on it slightly.

Here is my code:

#with  random forest
library(randomForest)

#how many trees 
ntree_list <- c(15,30,60,125,250,500)

#how many tests per tree
ntests <- 100

#prepare for loop
err <- as.data.frame(matrix(nrow = ntests, ncol=length(ntree_list)))

#main loop
#for each tree-size
for (i in 1:length(ntree_list)){
     
     names(err)[i] <- paste(as.character(ntree_list[i]),"tree",sep="_")
     
     #run a stack of tests
     for (j in 1:ntests){
          
          #fit the forest
          fit=randomForest(mpg~.,data=mtcars,ntrees = ntree_list[i])

          
          #pop the final error off the ensemble
          err[j,i] <- fit$mse[ntree_list[i]]
          
     }
}

You could, if you wanted, put other tree parameters in there instead of tree-count.

And now to plot the results:

#make plot
boxplot(err,notch=T,names=names(err), ylab = "MSE of Random forest",
        ylim = c(0, (range(mtcars$mpg)[2]-range(mtcars$mpg)[1])/2 ) )

grid()

This gives the following plot:

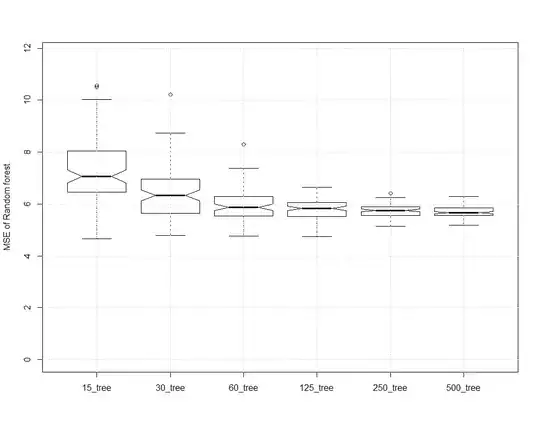
enter image description here

About the better, and agreeing with @hxd1011, eventually more trees doesn't do much good. It doesn't improve error. It does take more memory and cpu. You can observe that the 125 tree forest is, most of the time, pretty close to the MSE of the 500 tree forest.

When you start pruning, both by requiring at least so many samples to make a leaf, and by only allowing the tree to get so many levels deep, it substantially improves memory. A "not bad" start is 5 elements per leaf, and max depth of 8. This really is emprical and depends on the problem being solved.

If we change the code as follows:

n_list <- seq(from=1,to=29,by=1)
err <- as.data.frame(matrix(nrow = ntests, ncol=length(n_list)))
for (i in 1:length(n_list)){
names(err)[i] <- paste(as.character(n_list[i]),"count",sep="_")

          #fit the forest
          fit=randomForest(mpg~.,       #formula
                           data=mtcars, #data frame
                           ntrees = 125,
                           nodesize = n_list[i])

          
          #pop the final error off the ensemble
          err[j,i] <- fit$mse[125]

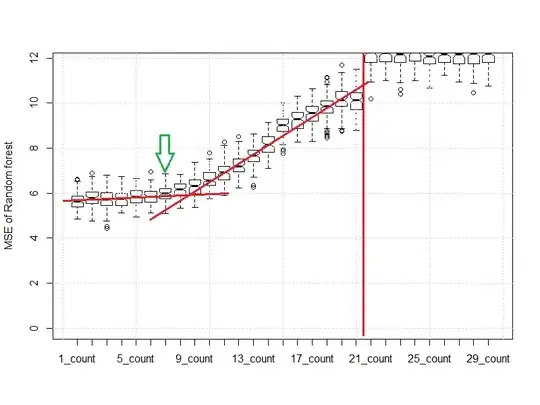
Then the plot changes as follows: enter image description here

You can see that when we use around 7 leaves per node, the MSE is still reasonably consistent with the "1" or "4" elements. If we had used 19 leaves, that requirement substantially impacts the MSE, and the MSE could be nearly double that of a "7" elements per leaf on tree rule.

The red lines are the mutant child of an eyeball norm and a scree plot. After 21 leaves per tree are required the RF becomes essentially no more useful than the midrange.

You can also do things like round the input data, or truncate digits. This allows less discrimination on inputs and can drive generalization. Take baby steps when doing this because while throwing away a little data can be a good thing, throwing away a lot of data is usually a bad thing.

Fun observation:

  • Breiman's randomForest beat h2o here. It takes much longer to do this exercise with h2o from today than with Breiman's work from a decade ago.
Sycorax
  • 76,417
  • 20
  • 189
  • 313
EngrStudent
  • 8,232
  • 2
  • 29
  • 82
  • 1
    great answer! Interestingly, I have tried many "revised random forest" model. Most models claim the original CART has biased feature selection problem and their tree are better in terms of unbiased feature selection. But in many real world data I worked with, it seems Brieman's original random forest is outperforming many modern models. – Haitao Du Jun 11 '16 at 00:45
3

  1. You should always have loss calculated to compare how good the model is. In regression the loss can be least square or least absolute value. You can compare how good the model is in a "testing data / validation data".

  2. mtry should be the only parameter you are tuning on.

  3. More trees is not "better", with sufficient number of trees, the "estimated testing error / out of bag error" will "converge". I personally never use more than 1000 trees. And you can observe when does it converge by plotting random forest.

    library(randomForest)

    fit=randomForest(mpg~.,data=mtcars)

    plot(fit)

enter image description here

Haitao Du
  • 32,885
  • 17
  • 118
  • 213
  • 1
    Thanks. Is there a way to plot the same thing with `ranger` ? – François M. Jun 10 '16 at 14:18
  • 1
    Number of trees should be driven by data. If you have many columns and many rows, and the relationship are complex, then you can "over-fit" later than 1000 trees. If you use a training and validation split then the oob error is not your only estimator for overfit. – EngrStudent Jun 10 '16 at 14:54
  • 1
    @EngrStudent I think there are many discussions about random forest "over fitting". My experience is that it seems does not over fit at all. Although there are signs like very low loss in training data, but in testing it seems fine. – Haitao Du Jun 10 '16 at 15:22
  • @hxd1011 I think you've been lucky. Random forest does overfit, particularly if you have large number of features. – horaceT Jun 11 '16 at 00:07
  • Thanks for your information @horaceT. Could you please give me some examples of over fitting? I found one [here](http://stats.stackexchange.com/questions/113177/random-forest-cant-overfit) – Haitao Du Jun 11 '16 at 00:48
  • @hxd1011 Sorry most examples are from my own modeling. But you could simulate "fat" datasets and I'm sure you'll see it very quickly. – horaceT Jun 11 '16 at 04:03
0

Random forest overfits too. It happened everytime I tried RF model. All the models I tried had more than 15 features to somewhere more than a couple of hundred. I have read in many places that it does not overfit but it does and sometimes by a big margin. Sometimes, it does really well on the development sample but really poorly on the validation. It depends on the data (noise level) and many other parameters.

Mahesh
  • 11
  • 1
  • 2
    1) Your answer makes unsupported assertions, not arguments. It would be improved if you could substantiate them. 2) The number of features being high does not imply overfitting; the RF uses all features that you give it. – mkt Aug 31 '17 at 07:20