2

I'm trying to classify (LDA) few samples (n=12) in a high dimensional feature space (p=24) into 3 classes.

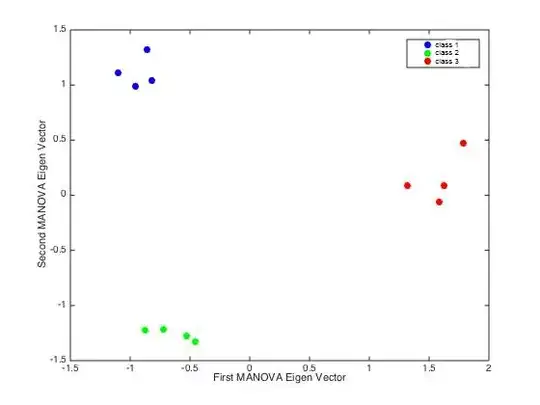
First I reduced the dimension of my initial dataset with a PCA, keeping only the first two Eigen vectors. Update: turns out, I was actually using all 11 PCs for the LDA. Then I had a look at the projection of my n x 2 n x 11 dataset in the LDA space (1st vs 2nd Eigen vector) and I obtained the following: Dataset projected in LDA space

I was quite happy because the LDA found a strong separation between the 3 classes.

So I tried a leave-one-out cross validation to evaluate the LDA. I trained the classifier with 11 samples and tested it with the last one, and looped around.

The problem is the classifier performs at chance level (30% success rate).

I noticed that the LDA space changes drastically between each iteration, depending on the 11 samples used to compute it. Moreover, when I project the tested sample in the corresponding LDA space, it falls quite far away from what should be its group, explaining the poor success rate. LDA space computed with 11 samples, and projection of the last one

My questions are: is it normal that such a (visually) nice separation between classes leads to such a poor classification? Is it due to the small number of samples? Is there anything I can do to improve the situation?

amoeba
  • 93,463
  • 28
  • 275
  • 317
Khanigh
  • 39
  • 3
  • LDA cannot work at all or work correctly in complete collinearity situation, such as when `n

     – ttnphns Jun 02 '16 at 17:47
  • Thank you for your answer! I tried to reduce p with a PCA, training the classifier only with the first two Eigen vectors. I still have a visually nice separation between classes, but the success rate remains at chance level. Is increasing N the only way out here? – Khanigh Jun 02 '16 at 18:04
  • Welcome to CV and congratulations with such a nicely written first post. +1. One thing is not clear to me: LDA computations require inverting within-class covariance matrix which in your $n

     – amoeba Jun 02 '16 at 20:19
  • You are absolutely right, I forgot to mention that I first reduced the dimension of the feature space with a MANOVA, training the classifier with the first two Eigen vectors. Hence, the pipeline is n x p initial dataset --> MANOVA --> n x 2 reduced dataset --> cross-validated LDA. I'll edit my post to add this information. I work with the Matlab function classify. – Khanigh Jun 02 '16 at 21:03
  • Sorry, Khanigh, this does not make much sense to me. What you call "reducing dimensionality with MANOVA" is usually called "reducing dimensionality with LDA" (MANOVA is equivalent to LDA, in this sense; "MANOVA space" and "LDA space" are the same thing). And I still maintain that it is not possible to do if $n

     – amoeba Jun 02 '16 at 21:06
  • Also, please use `@amoeba` somewhere in your reply, otherwise I will not get your message in my inbox. – amoeba Jun 02 '16 at 21:07
  • `reduced the dimension of the feature space with a MANOVA` Hmm, MANOVA isn't a space-reduction method itself. It is the very LDA (which is closely related to it) which can be thought of as a reduction tecnique. – ttnphns Jun 02 '16 at 21:09
  • @amoeba @ttnphns Sorry, it was late, I wrote MANOVA while thinking PCA. The pipeline is hence `n x p` initial dataset --> PCA --> `n x 2` reduced dataset --> cross-validated LDA. I've corrected the post. By the way, I came across this paper: [link](http://www.sciencedirect.com/science/article/pii/S0003267015008430) which proposes a regularized MANOVA for `n

     – Khanigh Jun 03 '16 at 09:43
  • Are you saying that the first figure you display in this post is actually PC1 vs PC2 of your whole dataset, with no LDA or MANOVA or anything like that involved in creating it? That's how I understood your last comment, but in the question text before the figure you say "Then I had a look at the projection of my nx2 dataset in the LDA space". But you already had a 2D space obtained with PCA? – amoeba Jun 03 '16 at 10:01
  • @amoeba Your last interpretation of my messy explanations (sorry!) is correct: I had a look at the projection of my nx2 dataset in the LDA space, 2 being PC1 and PC2 of the PCA previously performed. – Khanigh Jun 03 '16 at 10:20
  • But if you do LDA to extract 2 components from a 2-dimensional space (because you previously performed PCA to only have 2 components), then it will leave the space unchanged. Well - almost - the space can rotate and stretch, but in a way it will be the same space, the class separation will not change. However, something does not seem right here. Just to double-check, can you please post the PC1/PC2 scatterplot of your dataset, without any LDA? – amoeba Jun 03 '16 at 10:24
  • 1
    @amoeba Your comment made me realize that I wasn't feeding my LDA with only PC1 and PC2, but with the whole set of 11 PCs... Hence I think I am in the situation described in your answer to [this thread](http://stats.stackexchange.com/questions/106121/does-it-make-sense-to-combine-pca-and-lda?rq=1), i.e. over-fitting: near-perfect class separation on the training data with chance performance on the test data. Am I right? Anyway thank you very much for your help! – Khanigh Jun 03 '16 at 10:59
  • Yes, that's what I have been suspecting. You can try to use PCA+LDA or regularized LDA to try to tackle your problem. But you should decide what to do with this question. If you still want an answer, please edit to update or clarify. Or we can close it as a duplicate of that one. – amoeba Jun 03 '16 at 11:12
  • 1
    @amoeba Yes, I don't think my problem is different enough from the thread I mentioned to justify a distinct post. We can close it. – Khanigh Jun 03 '16 at 12:02

0 Answers0