Show estimate converges to percentile through order statistics

Question

Let $X_1, X_2, \ldots, X_{3n}$ be a sequence of iid random variables sampled from an alpha stable distribution, with parameters $\alpha = 1.5, \; \beta = 0, \; c = 1.0, \; \mu = 1.0$.

Now consider the sequence $Y_1, Y_2, \ldots, Y_{n}$, where $Y_{j+1} = X_{3j+1}X_{3j+2}X_{3j+3} - 1$, for $j=0, \ldots, n-1$.

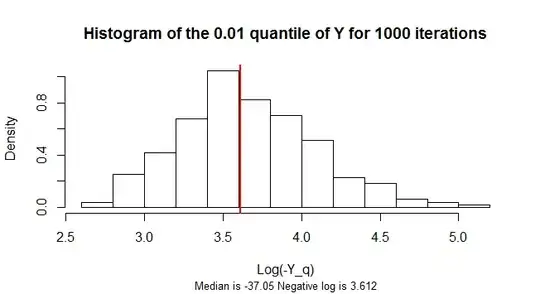
I want to estimate the $0.01-$percentile.

My idea is to perform sort of a Monte-Carlo simulation:

l = 1;
while(l < max_iterations)
{
  Generate $X_1, X_2, \ldots, X_{3n}$ and compute $Y_1, Y_2, \ldots, Y_{n}$;
  Compute $0.01-$percentile of current repetition;
  Compute mean $0.01-$percentile of all the iterations performed;
  Compute variance of $0.01-$percentile of all the iterations performed;
  Calculate confidence interval for the estimate of the $0.01-$percentile;

  if(confidence interval is small enough)
    break;

}

Calling the mean of all the sample $0.01-$percentiles computed to be $\hat{\mu}_n$ and their variance $\hat{\sigma}^{2}_{n}$, to compute the appropriate confidence interval for $\mu$, I resort to the Strong form of the Central Limit Theorem:

Let $X_1, X_2, \ldots$ be a sequence of iid random variables with $E \left[ X_i \right] = \mu$ and $0 < V \left[ X_i \right] = \sigma^2 < \infty$. Define the sample mean as $\hat{\mu}_n = (1/n) \sum_{i=1}^n X_i$. Then, $(\hat{\mu}_n - \mu) / \sqrt{\sigma^{2}/n}$ has a limiting standard normal distribution, i.e. $$ \frac{\hat{\mu}_n - \mu}{\sqrt{\sigma^{2}/n}} \overset{n \rightarrow \infty} \longrightarrow N(0,1).$$

and Slutksy's theorem to conclude that $$ \sqrt{n} \frac{\hat{\mu}_n - \mu}{\sqrt{\hat{\sigma}^{2}_{n}}} \overset{n \rightarrow \infty} \longrightarrow N(0,1).$$

Then a $(1-\alpha)\times 100\%$-confidence interval for $\mu$ is

$$ I_{\alpha} = \left[\hat{\mu}_n - z_{1- \alpha / 2} \sqrt{\frac{\hat{\sigma}^{2}_{n}}{n}} , \hat{\mu}_n + z_{1- \alpha / 2} \sqrt{\frac{\hat{\sigma}^{2}_{n}}{n}} \right], $$ where $z_{1- \alpha / 2}$ is the $(1- \alpha / 2)$-quantile of the standard normal distribution.

---

Questions:

1) Is my approach correct? How can I justify the application of the CLT? I mean, how can I show that the variance is finite? (Do I have to look at the variance of $Y_j$? Because I don't think it is finite...)

2) How can I show that the average of all the sample $0.01-$percentiles computed converges to the true value of the $0.01-$percentile? (I should use order statistics but I'm unsure on how to procceed; references are appreciated.)

Answer 1

The variance of $Y$ is not finite. This is because an alpha-stable variable $X$ with $\alpha=3/2$ (a Holtzmark distribution) does have a finite expectation $\mu$ but its variance is infinite. If $Y$ had a finite variance $\sigma^2$, then by exploiting the independence of the $X_i$ and the definition of variance we could compute

$$\eqalign{ \sigma^2 = \operatorname{Var}(Y) &= \mathbb{E}(Y^2) - \mathbb{E}(Y)^2 \\ &= \mathbb{E}(X_1^2X_2^2X_3^2) - \mathbb{E}(X_1X_2X_3)^2 \\ &= \mathbb{E}(X^2)^3 - \left(\mathbb{E}(X)^3\right)^2 \\ &= \left(\operatorname{Var}(X) + \mathbb{E}(X)^2\right)^3 - \mu^6 \\ &= \left(\operatorname{Var}(X) + \mu^2\right)^3 - \mu^6. }$$

This cubic equation in $\operatorname{Var}(X)$ has at least one real solution (and up to three solutions, but no more), implying $\operatorname{Var}(X)$ would be finite--but it's not. This contradiction proves the claim.

---

Let's turn to the second question.

Any sample quantile converges to the true quantile as the sample grows large. The next few paragraphs prove this general point.

Let the associated probability be $q=0.01$ (or any other value between $0$ and $1$, exclusive). Write $F$ for the distribution function, so that $Z_q=F^{-1}(q)$ is the $q^{\text{th}}$ quantile.

All we need to assume is that $F^{-1}$ (the quantile function) is continuous. This assures us that for any $\epsilon\gt 0$ there are probabilities $q_-\lt q$ and $q_+\gt q$ for which

$$F(Z_q - \epsilon) = q_-,\quad F(Z_q + \epsilon) = q_+,$$

and that as $\epsilon\to 0$, the limit of the interval $[q_-, q_+]$ is $\{q\}$.

Consider any iid sample of size $n$. The number of elements of this sample that are less than $Z_{q_-}$ has a Binomial$(q_-, n)$ distribution, because each element independently has a chance $q_-$ of being less than $Z_{q_-}$. The Central Limit Theorem (the usual one!) implies that for sufficiently large $n$, the number of elements less than $Z_{q_-}$ is given by a Normal distribution with mean $nq_-$ and variance $nq_-(1-q_-)$ (to an arbitrarily good approximation). Let the CDF of the standard Normal distribution be $\Phi$. The chance that this quantity exceeds $nq$ therefore is arbitrarily close to

$$1-\Phi\left(\frac{nq - nq_-}{\sqrt{nq_-(1-q_-)}}\right) = 1-\Phi\left(\sqrt{n}\frac{q - q_-}{\sqrt{q_-(1-q_-)}}\right).$$

Because the argument on $\Phi$ on the right hand side is a fixed multiple of $\sqrt{n}$, it grows arbitrarily large as $n$ grows. Since $\Phi$ is a CDF, its value approaches arbitrarily close to $1$, showing the limiting value of this probability is zero.

In words: in the limit, it is almost surely the case that $nq$ of the sample elements are not less than $Z_{q_-}$. An analogous argument proves it is almost surely the case that $nq$ of the sample elements are not greater than $Z_{q_+}$. Together, these imply the $q$ quantile of a sufficiently large sample is extremely likely to lie between $Z_q-\epsilon$ and $Z_q+\epsilon$.

That's all we need in order to know that simulation will work. You may choose any desired degree of accuracy $\epsilon$ and confidence level $1-\alpha$ and know that for a sufficiently large sample size $n$, the order statistic closest to $nq$ in that sample will have a chance at least $1-\alpha$ of being within $\epsilon$ of the true quantile $Z_q$.

---

Having established that a simulation will work, the rest is easy. Confidence limits can be obtained from limits for the Binomial distribution and then back-transformed. Further explanation (for the $q=0.50$ quantile, but generalizing to all quantiles) can be found in the answers at Central limit theorem for sample medians.

The $q=0.01$ quantile of $Y$ is negative. Its sampling distribution is highly skewed. To reduce the skew, this figure shows a histogram of the logarithms of the negatives of 1,000 simulated samples of $n=300$ values of $Y$.

library(stabledist)
n <- 3e2
q <- 0.01
n.sim <- 1e3

Y.q <- replicate(n.sim, {
  Y <- apply(matrix(rstable(3*n, 3/2, 0, 1, 1), nrow=3), 2, prod) - 1
  log(-quantile(Y, 0.01))
})
m <- median(-exp(Y.q))
hist(Y.q, freq=FALSE, 
     main=paste("Histogram of the", q, "quantile of Y for", n.sim, "iterations" ),
     xlab="Log(-Y_q)",
     sub=paste("Median is", signif(m, 4), 
               "Negative log is", signif(log(-m), 4)),
     cex.sub=0.8)
abline(v=log(-m), col="Red", lwd=2)