5

$X_1,X_2,..,X_n$ is a random sample from the random variable whose pdf is, \begin{align*} f(x)=\lambda e^{-\lambda(x-\mu)},\mu<x<\infty \end{align*} How can we find $E(X_{(2)}-X_{(1)})$, if $n=2?$

We know that,$f_{X(r)}(x)=\frac{n!}{(n-r)!(r-1)!}F(x)^{r-1}(1-F(x))^{n-r}f(x)$

Here,$r=2,n=2$

$\rightarrow f(X_{(2)}(x)=2\lambda^{2}[e^{\lambda\mu-\lambda x}-e^{-2\lambda x+\lambda\mu}]$

It is difficult to compute, $E(X_{(2)})=\int_{\mu}^\infty 2x\lambda^{2}[e^{\lambda\mu-\lambda x}-e^{-2\lambda x+\lambda\mu}]dx$

I have also tried to find, $E(X_{(2)})=\int_{\mu}^{\infty}[1-F(x_{(r)})]dx$

Similar problem arises in case of $E(X_{(1)})$ too.

priyanka
  • 760
  • 5
  • 17

2 Answers2

5

As explained at The Number of Exponential Summands in a Fixed Interval is Poisson, each of the variables $X_i$ is the waiting time for the first point to appear in a Poisson process of rate $\lambda$ starting at time $\mu$. It is obvious from the characteristic properties of a Poisson process that a union of Poisson processes of rates $\lambda_1, \lambda_2, \ldots, \lambda_n$ is just a Poisson process of rate $\lambda_1+\lambda_2+\cdots+\lambda_n$, equal to $n\lambda$ in this case. Therefore the expected waiting time to the first point among them all must be $1/(n\lambda)$.

After the first time $X_{(1)}$ is encountered, there remain samples from the $n-1$ other processes. Since they are all independent, and the chance of new points appearing is independent of any previous points that have appeared, it's the same situation all over again: the starting time is now $X_{(1)}$ instead of $\mu$ and $n$ has decreased to $n-1$, that's all. Consequently the expected time to wait for the next point, which is $X_{(2)}-X_{(1)}$, is $1/(\lambda(n-1))$.

(And so it continues: the expectation of $X_{(j+1)}-X_{(j)}$ is $1/(\lambda(n-j))$ for $j=1, 2, ..., n-1$.)

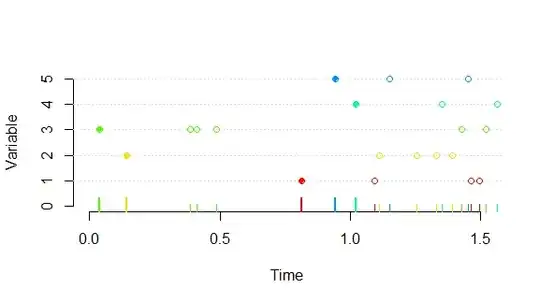
Figure

In this figure a realization of a Poisson process of rate $\lambda=2$ is shown for each of $n=5$ independent variables indexed $1$ through $5$. The union of the points is plotted with ticks at the bottom: they form a realization of a Poisson process of rate $n\lambda=10$. The first points in each process are highlighted with solid dots (and shown with longer ticks at the bottom): these form the sample $(X_1, X_2, \ldots, X_n)$; all the hollow dots are superfluous but are shown to illustrate the concepts. The expected time to wait for the very first point overall is $1/(n\lambda)=1/10$ because the combined rate is $n\lambda$. After it is encountered, four processes remain. Thus, their combined rate is $(n-1)\lambda=8$ and the expected waiting time to the first point among them is $1/((n-1)\lambda)=1/8$.

Community
  • 1
whuber
  • 281,159
  • 54
  • 637
  • 1,101
0

if you look at the $\mu$ parameter of your density, this is a location parameter and can be restated as follows:

$X = Y+\mu , \text{where Y~Exp}(\lambda)$

now

$F_{X_{(1)}}(x)=1-(1-F_X(x))^2 = 1-(e^{-\lambda(x-\mu)})^2 = 1-e^{-2\lambda (x-\mu)}$

the minimum is only an exponential random variable intensity $2\lambda$ plus $\mu$

$X_{(1)} = W+\mu , \text{where W~Exp}(2\lambda)$

then $E[X_{(1)}]=\frac{1}{2\lambda}+\mu$

now $E[X_{(1)}+X_{(2)}]=E[X_1+X_2]=\frac{2}{\lambda}+2\mu$ because your variables can be decomposed as before

now $E[X_{(2)}-X_{(1)}]=E[X_{(1)}+X_{(2)}]-2E[X_{(1)}]=\frac{2}{\lambda}+2\mu-2(\frac{1}{2\lambda}+\mu)= \frac{1}{\lambda}$

You can also use the change of variable y = x-mu, the integrals are simplified in terms of densities and expected values Exponential

JavierMtz
  • 26
  • 2