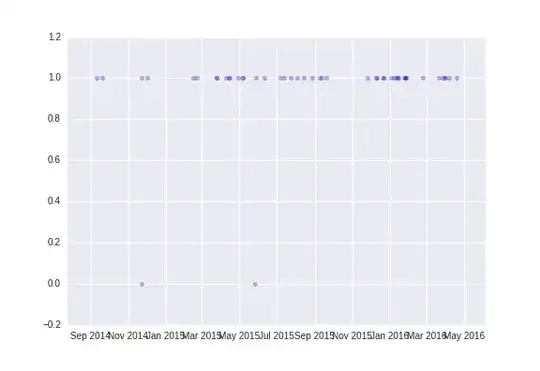
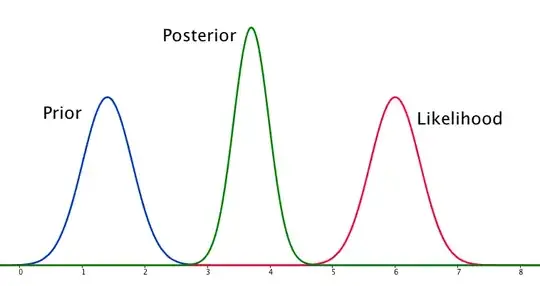
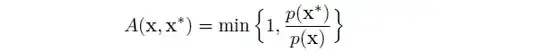I have a dependent binary variable Y, and an independent date variable X. I want to find out if there is any seasonality (at the year level).
A few notes:
The binary variable is in my model non-deterministic, but I believe may have a higher probability of being 1 given the point in the season. (This maybe obvious but feels important to make clear.)
There are usually 0, 1 or very few data points for each date.
There is only about two years worth of data.
There may be one or more underlying trends that need to be accounted for.