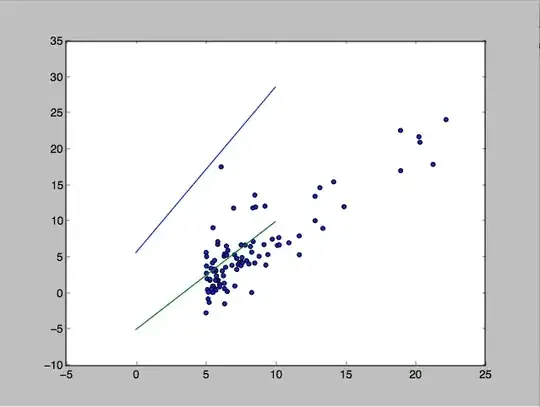
Based on the Coursera Course on Machine Learning, I implemented batch gradient descent using python. The progression of $J(\theta)$ is expectedly decreasing (which suggests that my implementation is correct), but the final $\theta$ given by my implementation yields the blue line below, with a cost of ~12, while a more reasonable fit given by the green line below has a cost of ~72.
How can this be?
Here is the data I used:https://justpaste.it/ulce
And the cost function: $\frac{1}{2m}\sum_{i = 1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})^{2}$
implemented in python as:
def costFunction(x, y, theta):
sum = 0
for i in range(len(x)):
sum += (np.dot(x[i,:],theta) - y[i])**2
return (sum/(len(x) *2))
The data can be accessed here:
library(gsheet)
data <- read.csv(text =
gsheet2text('https://docs.google.com/spreadsheets/d/12AwTiqx_IJzhFqp3baMk3LxvYr2gUCA73RUCI5tTXhw/edit?usp=sharing',
format ='csv'))
UPDATE:
My implementation works well when I don't preprocess the data. My process of "extrapolating" $\theta$ (if I preprocess) must be poor. This is what I did:
I transform every sample in the feature (there is only one feature) using:
$X_{\alpha} = \frac{X - X_{min}}{X_{max} - X_{min}}$
These are then the relevant values to extrapolate:
$\theta = [5.670, 2.301] = [\theta_{0}, \theta{1}]$
$X_{min} = 5.0269$
$X_{max} = 22.203$
When I go to plot, I simply plot $(X, h_{\theta}(X_{\alpha}))$:
x = pylab.linspace(0,30, num = 1000)
x1 = (x - 5.0269)/(22.203 - 5.0269)
y = 5.67002243 + 2.301*x1
plt.plot(x,y)