2

Simple question:

Is there a rule of thumb for number of bins in a histogram with a uniform distribution?

Details:

I have a stochastic computer simulation that produces, as a test, $n$ values that should be uniformly distributed in a given interval, $[a, b]$. Due to the inherent random nature of the simulation, there is some noise.

I want to show (visually) that under certain circumstances there is additionally a deviation from this uniform distribution. The deviation happens at the lower boundary, up to $5$ to $15$% of the interval and manifests as less values (up to about $40$%) per bin as a uniform distribution would have.

At the moment $n=5\times10^6$, but I can increase that if necessary. To simplify the comparison between different cases that don't have the same $a$ and $b$ I scale to $[0, 1]$. This is standard practice in my field.

My idea is to use a histogram, but I've been trying to find a justifiable method to define the bin size (or number of bins) and failed so far. Most rules-of-thumb I found assume a normal distribution. Is there any that uses uniform distribution? It's bad to search for, because I only find discussion about uniform bin size, not uniform distribution.

The best rules I can find from wikipedia are:
Freedman-Diaconis $\approx 160$
Doane-Rule $\approx 20$
The difference lies most likely in the skewness, which is very close to zero in my cases, or I simply used the formula wrong. It's apparently not that simple. What I did (in Python):
k = 1 + numpy.log2(n) + numpy.log2(1 + abs(scipy.stats.skew(z, bias=False)) / np.sqrt(6 * (n - 2) / ((n + 1) * (n + 3))))

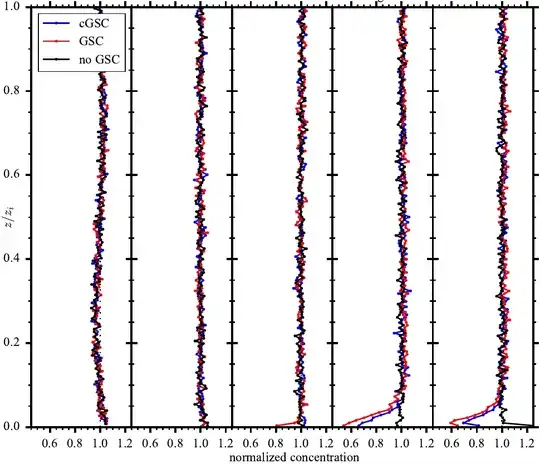
Purely subjectively I'd say that $20$ is far too few and $160$ is ok, but Freedman-Diaconis is built on the assumption of normal distributed values... This is an example with 160 bins. I want to show the difference between the black, blue and red line at the bottom for panels (3)-(5), which are not there for (1) and (2). I'm aware that connecting histogram values with a straight line is terrible from a mathematical standpoint, but there are extenuating circumstances that make this a little bit better (basically the values represent a concentration field, which is continuous).

example image with 160 bins

Edit1: I forgot to mention: plotting the independent variable on the second axis is standard practice in my field, because it's the height. So the histogram is turned by $90°$ compared to the usual way.

Edit2: An example P-P-plot (the rightmost panel in the figure above), as suggested by whuber: 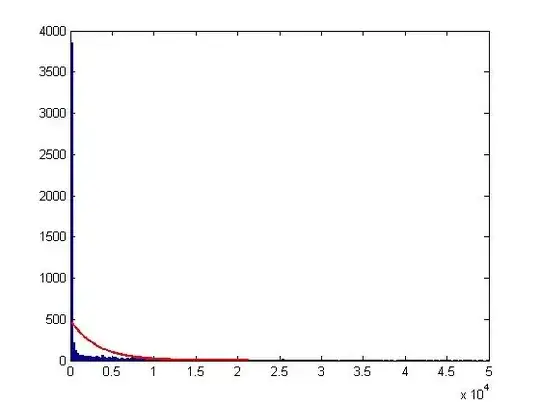enter image description here For me it is a lot harder to interpret, but that might be my problem, not true in general.

Edit3: This question is different, because it (i) looks for an automated solution (which I don't) and (ii) it does not have an underlying (almost) uniform distribution.

StefanS
  • 183
  • 5
  • 1
    Why not use a more powerful graphical method such as a probability plot? – whuber May 23 '16 at 22:30
  • @whuber, to be honest, I didn't think of that. You are right, that circumvents the problem with the bin size, but then I have 1.5 million points in each panel. The only way I can think of to reduce that is by binning the data. The physical interpretation is (at least for me, as a non-statistician) also a lot more complicated, because the deviation from uniformity is not just visible where it actually happens, but also everywhere after that. So you can't just look at the value, you have to look at the slope of the curve. I'll edit in a quick mock-up. – StefanS May 24 '16 at 09:45
  • @stefan - so it takes a little while to render? Is 60 seconds going to hurt that much? Tools like JMP handle those sample sizes well. You could also bootstrap resample the distribution. You could sort then use EWMA to compute both the mean and variance. Spikes in the (Bollinger) variance should tell you when you have atypical departures from the mean. – EngrStudent May 24 '16 at 10:08
  • @EngrStudent - Well, when I save the mock-up as pdf (vector graphics), it takes about 2 minutes to open in Okular, and that's just 1/5 of the total plot. I can't put that in a paper. But you are right, I could work around that by rasterizing the figure. What would bootstrap resampling help? I had to look up EWMA and found that its built on normal distribution. Isn't that a problem for my application? I also couldn't find Bollinger variance, only Bollinger bands, which do not seem applicable here. – StefanS May 24 '16 at 11:06
  • Also, I just realized that both EWMA and Bollinger Bands require a time series (or at least an independent and a dependent variable). I don't have that, just an array of values that should be uniformly distributed. – StefanS May 24 '16 at 11:17
  • 1.5 million points is fairly large, but 15000 (say) is quite manageable. You can reduce your data to that amount in several simple ways. One is by subsampling: sort them and retain every (say) hundredth value. Another is by windowing: since you are concerned about behavior near the "lower boundary," simply display the part of the probability plot in that region. You may combine these two techniques. – whuber May 24 '16 at 11:46
  • @whuber: Do I not lose a power by subsampling? As I said, I have a stochastic model and try to circumvent the counter-argument "the feature you are showing just happened randomly, not due to any underlying process". This interpretation is definitely possible, just highly unlikely the more samples I show or average over. Windowing is an idea, but that takes away the information that this does not happen at the upper boundary (not clear a priori) and in-between (good to know). What do you think of using a kernel density estimation? Although there's the problem with selecting the bandwidth... – StefanS May 24 '16 at 12:49

0 Answers0