Your question is somewhat problematic, because for a given probability $$\Pr[X = k] = p(1-p)^k$$ and a given $k$, there are in general two distinct solutions $p \in (0,1)$ that will satisfy the condition. Only when $p = (1+k)^{-1}$ (corresponding to the probability $\Pr[X = k] = k^k (1+k)^{-(1+k)}$) will you have a unique solution. To see why, observe that on $p \in (0,1)$, the derivative of the probability mass function with respect to $p$ is $$\frac{d}{dp}\left[p(1-p)^k\right] = -(kp+p-1)(1-p)^{k-1}.$$ The term $(1-p)^{k-1}$ is positive for all $k \in \mathbb Z^+$. The other factor is zero whenever $p = (k+1)^{-1}$ as stated previously, corresponding to a global maximum on $(0,1)$; as this factor $kp+p-1$ is a linear function of $p$, it therefore demonstrates that $\Pr[X = k]$ is increasing for $0 < p < 1/(1+k)$, and decreasing for $1/(1+k) < p < 1$. Hence there will be in general one solution in each such interval.
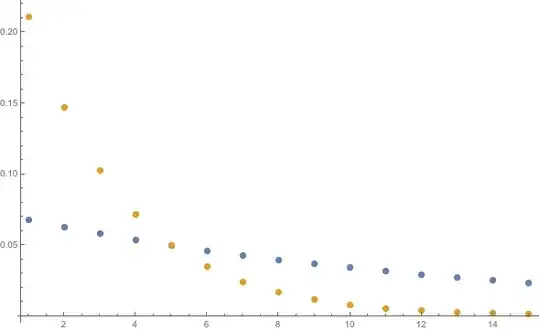
For example, suppose we are given $X \sim \operatorname{Geometric}(p)$ and $\Pr[X = 5] = 1/20$. Then we can numerically verify that $$p \approx \{0.0730689462638205, 0.302187628494614\}$$ both work. A plot of the resulting PMFs are shown for $k \in \{1, \ldots, 15\}$: