I have been studying 2x2 contingency tables and specifically I have been looking at situations where the marginals are fixed by design for one categorical variable.
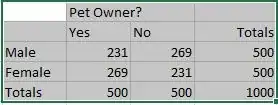
As an example, suppose a researcher is interested in evaluating whether there is a significant difference in the proportion of male vs female pet owners in a large city. The research performs separate, independent random samples on 500 males and 500 females. The results are summarized in the 2x2 table below.
I realize the standard test for homogeneity would be a chi-square test or z-test for difference in proportions (with continuity corrections). When I calculate this I get a p-value of 0.019279. I also performed the Fisher Exact Test (FET) which returns a p-value of 0.019234. Intuitively it makes sense to me that these two tests would produce very nearly the same result, reflecting I think the fact that the hypergeometric distribution converges to a normal distribution for large sample sizes. So far so good....
However, it seems to me that what we really have are two binomial samples, both with sample size of 500. If we are testing the null hypothesis that the proportion of male pet owners is equal to the proportion of female pet owners (vs. alternative that they are not equal), and we further assume that the overall population proportion of pet owners is 0.5 consistent with our sample (which is what a z-test of difference in proportions also assumes), my thinking is that we should be able to calculate the probability of all possible results as the product of 2 binomials, and sum all of these probabilities that are equal to or lower than the probability for the result we obtained from our samples to obtain a p-value. When I do this, I obtain a p-value of 0.056987.
My questions are as follows:
1 Do the p-values I calculate look correct? I have confidence in the calculations for the z-test/chi-square and FET, but the calculation of the p-value using the product of binomials approach I would have expected to also be very close to these other tests so I am concerned there is an error in my calculations (using excel spreadsheet).
Is the product of 2 binomials a valid approach given the circumstances? If so, is it correct to sum all cases where the probability is < or = to the specific probability of obtaining the specific sample results as depicted in the table (as with FET)?
Is it correct to expect that for large samples the p-value should be very nearly equal to the z-test/chi-square test results?
I originally was investigating the product binomial approach for small samples as an alternative to FET, and noticed substantial differences in p-values for many cases. But I had hoped to see convergence of p-values for all these tests for large samples, but results above make me think there is a fundamental flaw in either my thinking or calculations or both!